Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

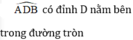
⇒ A B t ^ = 1 2 . s đ A B ⏜ + s đ M N ⏜ > 1 2 . s đ A B ⏜ = A C B ^

a) Trong tứ giác AOBM có 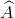 =
=  =
=  .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 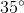
= 
b) Từ 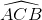 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 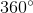 -
-  =
= 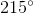

M1 là điểm bất kì nằm trong cung chứa góc 550 (hình a).
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương) Vậy góc AM1B > 550
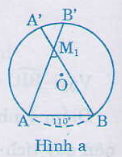
b)
M2 là điểm bất kì nằm ngoài đường tròn (h.b), M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
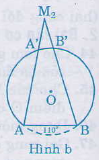
M1 là điểm bất kì nằm trong cung chứa góc 550 .
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương)
Vậy góc AM1B > 550
b)
M2 là điểm bất kì nằm ngoài đường tròn , M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
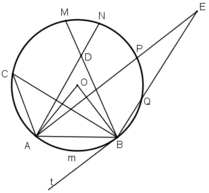
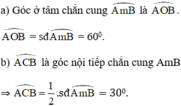

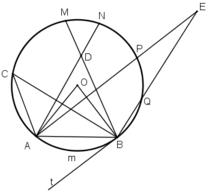

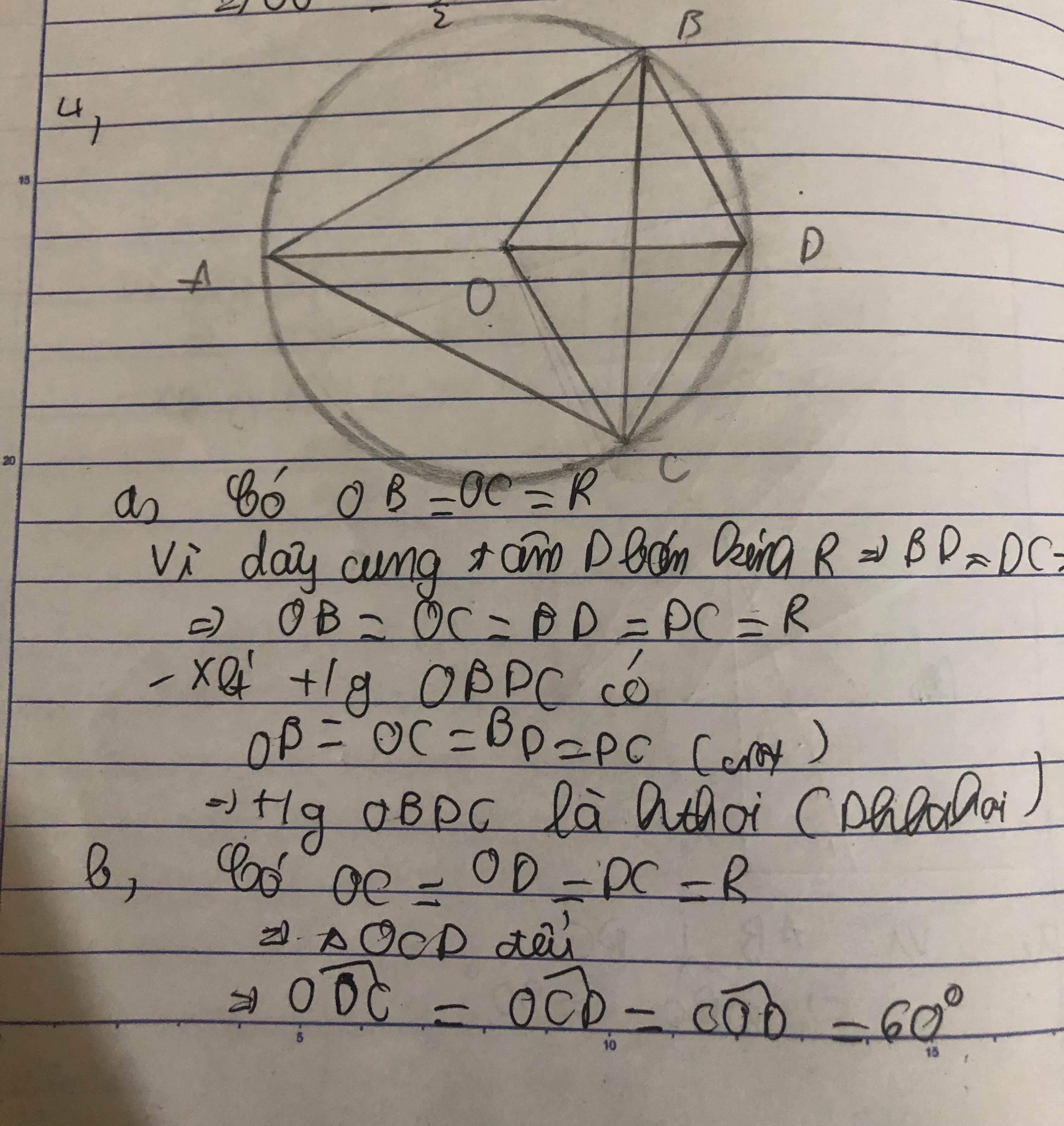
Trong hình 67, cung AmB có số đo là 66o. Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ˆADBADB^ với ˆACBACB^ .
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh ˆAEBAEB^ với ˆACBACB^
Hướng dẫn trả lời:
a) Từ O nối với hai đầu mút của cung AB
Ta có ˆAOBAOB^ là góc ở tâm chắn cung AB
Vì ˆAOBAOB^ là góc ở tân chắn cung AB nên
ˆAOBAOB^ = sđ cung AB = 60°
b) Lấy một điểm C bất kì trên (O). Nối C với hai đầu mút của cung AmB. Ta được góc nội tiếp ˆACBACB^
Khi đó: ˆACB=12sđcungAmB=12600=30ACB^=12sđcungAmB=12600=30
c) Vẽ bán kính OB. Qua B vẽ Bt ⊥ OB. Ta được góc Abt là góc tạo bởi tia tiếp tuyến Bt với dây cung BA.
Ta có: ˆABt=12sđcungAmB=300ABt^=12sđcungAmB=300
d) Lấy điểm D bất kì ở bên trong đường tròn (O). Nối D với A và D với B. ta được góc là góc ở bên trong đường tròn (O)
Ta có:
ˆACB=12sđcungAmBˆADB=12(sđcungAmB+sđcungCK)ACB^=12sđcungAmBADB^=12(sđcungAmB+sđcungCK)
Mà sđcung AmB + sđcung CK > sđcung AmB (do sđcung CK > 0) nên ˆADB>ˆACBADB^>ACB^
e) Lấy điểm E bất kì ở bên ngoài đường tròn, nối E với A và E với B, chúng cắt đường tròn lần lượt tại J và I.
Ta có góc AEB là góc ở bên ngoài đường tròn (O)
Có:
ˆACB=12sđcungAmBˆAEB=12(sđcungAmB−sđcungIJ)ACB^=12sđcungAmBAEB^=12(sđcungAmB−sđcungIJ)
Mà sđcung AmB – sđ cung IJ < sđcung AmB (do sđcung IJ > 0)
Nên ˆAEB<ˆACBAEB^<ACB^