Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ����ABCD là hình bình hành.
b) �,�,�P,N,Q thẳng hàng.
c) Δ���ΔABC cần thêm điều kiện gì để tứ giác ����ABCD là hình vuông.

a) Vì ��=2��AB=2BC suy ra ��=��2=��BC= AB/2=AD
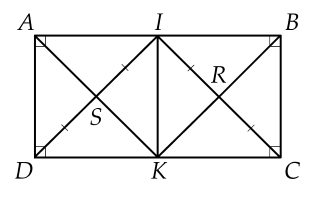
ABCD là hình chữ nhật nên AB=DC suy ra 1/2AB=1/2DC do đó AI=DK=AD
Tứ giác AIKD có AI//DK, AI=DK nên tứ giác AIKD là hình bình hành
Lại có AD=AI nên AIKD là hình thoi
Mà góc IAD= 90 độ do đó AIKD là hình vuông
Vậy tứ giác AIKD là hình vuông
Chứng minh tương tự cho tứ giác BIKC
Vậy tứ gáic BIKC là hình vuông
b) VÌ AIKD là hình vuông nên DI là tia phân giác góc ADK nên góc IDK = 45 độ
Tương tự góc ICK = 45 độ
Tam giác IDC cân có góc DIC = 90 độ nên là tam gaic vuông cân
Vậy tam giác IDC là tam gáic vuông cân
c) Vì AIKD, BCKI là các hình vuông nên hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên SI=SK=DI/2 và IR=RK=IC/2
=>ISKR là hình thoi
Lại có góc DIC= 90 độ nên ISKR là hình vuông
Vậy ISKR là hình vuông

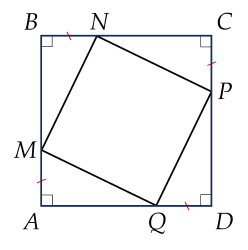
a) Do ABCD là hình vuôn nên:
\(AB=BC=CD=AD\)
Mà: \(\left\{{}\begin{matrix}AB=AM+MB\\BC=BN+NC\\CD=CP+PD\\AD=DQ+QA\end{matrix}\right.\)
Lại có: \(AM=BN=CP=DQ\)
\(\Rightarrow MB=NC=PD=QA\left(dpcm\right)\)
b) Xét \(\Delta QAM\) và \(\Delta NCP\) có:
\(\widehat{A}=\widehat{C}=90^o\left(gt\right)\)
\(AM=CP\left(gt\right)\)
\(QA=NC\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP\left(c.g.c\right)\)
c) Xét các tam giác: \(\Delta QAM,\Delta NCP,\Delta PDQ,\Delta MBN\) ta có:
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\left(gt\right)\)
\(AM=BN=CP=DQ\left(gt\right)\)
\(MB=NC=PD=QA\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP=\Delta PDQ=\Delta MBN\left(c.g.c\right)\)
\(\Rightarrow MQ=QP=PN=NM\) (các cạnh tương ứng)
\(\Rightarrow MNPQ\) là hình thoi (1)
Xét tam giác QAM ta có:
\(\widehat{QMA}+\widehat{AQM}=180^o-90^o=90^o\)
Mà: \(\Delta QAM=\Delta MBN\left(cmt\right)\)
\(\Rightarrow\widehat{BMN}=\widehat{AQM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{BMN}+\widehat{QMA}=90^o\)
Lại có: \(\widehat{BMN}+\widehat{QMA}+\widehat{NMQ}=180^o\)
\(\Rightarrow\widehat{NMQ}=180^o-90^o=90^o\) (2)
Từ (1) và (2) ta có MNPQ là hình vuông
a) ����ABCD là hình vuông nên ��=��=��=��AB=BC=CD=DA
Mà ��=��=��=��AM=BN=CP=DQ.
Trừ theo vế ta được ��−��=��−��=��−��=��−��AB−AM=BC−BN=CD−CP=DA−DQ
Suy ra ��=��=��=��MB=NC=PD=QA
Xét tam giác QAM và tam giác NPC có:
góc A = góc C = 90 độ
AQ=NC(cmt)
AM=CP(gt)
=>Tam giác QAM= tam giác NPC(c.g.c)
c)=> NP = MQ ( hai cạnh tương ứng)
Chứng minh tương tự như phần b ta có: Tam giác QAM= tam giác PDQ và tam giác QAM= tam giác MBN
Khi đó: MQ=PQ, MN=MQ và góc AMQ= góc DQP
Mà góc AMQ+AQM=90 độ
=>góc DQP+ góc AQM= 90 độ
Do đó góc MQP = 90 độ
tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi
Lại có góc MQP = 90 độ nên là hình vuông
Vậy tứ giác MNPQ là hình vuông

a/
Ta có
IA=IC (gt); IM=IK (gt) => AMCK là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
MB=MC (gt); IA=IC (gt) => MI là đường trung bình của tg ABC => MI//AB
Mà \(AB\perp AC\)
\(\Rightarrow MI\perp AC\Rightarrow MK\perp AC\)
=> AMCK là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
b/
Ta có
MI//AB (cmt) => MK//AB
AK//MC (cạnh đối hbh AMCK) => AK//MB
=> AKMB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Để AMCK là hình vuông \(\Rightarrow AM\perp BC\) => AM là đường cao của tg ABC
Mà AM là trung tuyến của tg ABC (gt)
=> ABC cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến là tg cân)
=> Để AMCK là hình vuông thì tg ABC vuông cân tại A
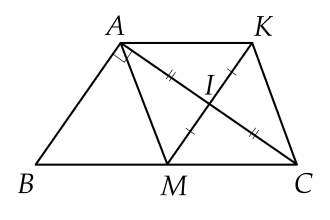
a) Tứ giác ����AMCK có hai đường chéo ��,��AC,MK cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Δ���ΔABC vuông tại �A có ��AM là đường trung tuyến nên ��=��=��AM=MC=MB.
Vậy hình bình hành ����AMCK có ��=��AM=MC nên là hình thoi.
b) Vì ����AMCK là hình thoi nên ��AK // ��BM và ��=��=��AK=MC=BM.
Tứ giác ����AKMB có ��AK // ��,��=��BM,AK=BM nên là hình bình hành.
c) Để ����AMCK là hình vuông thì cần có một góc vuông hay ��⊥��AM⊥MC.
Khi đó Δ���ΔABC có ��AM vừa là đường cao vừa là đường trung tuyến nên cân tại �A.
Vậy Δ���ΔABC vuông cân tại �A thì ����AMCK là hình vuông.

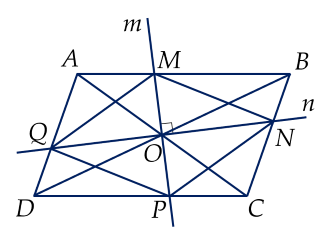
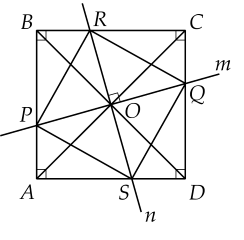
a) ����ABCD là hình bình hành nên hai đường chéo ��,��AC,BD cắt nhau tại �O là trung điểm của mỗi đường.
Xét Δ���ΔOBM và Δ���ΔODP có:
��=��OB=OD ( giả thiết)
���^=���^OBM=ODP (so le trong)
���^=���^BOM=DOP (đối đỉnh)
Vậy Δ���=Δ���ΔOBM=ΔODP (g.c.g)
Suy ra ��=��OM=OP (hai cạnh tương ứng)
Chứng minh tương tự Δ���=Δ���ΔOAQ=ΔOCN (g.c.g) suy ra ��=��OQ=ON (hai cạnh tương ứng)
����MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành ����MNPQ có hai đường chéo ��⊥��MP⊥NQ nên là hình thoi.
a) ����ABCD là hình bình hành nên hai đường chéo ��,��AC,BD cắt nhau tại �O là trung điểm của mỗi đường.
Xét Δ���ΔOBM và Δ���ΔODP có:
��=��OB=OD ( giả thiết)
���^=���^OBM=ODP (so le trong)
���^=���^BOM=DOP (đối đỉnh)
Vậy Δ���=Δ���ΔOBM=ΔODP (g.c.g)
Suy ra ��=��OM=OP (hai cạnh tương ứng)
Chứng minh tương tự Δ���=Δ���ΔOAQ=ΔOCN (g.c.g) suy ra ��=��OQ=ON (hai cạnh tương ứng)
����MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành ����MNPQ có hai đường chéo ��⊥��MP⊥NQ nên là hình thoi.

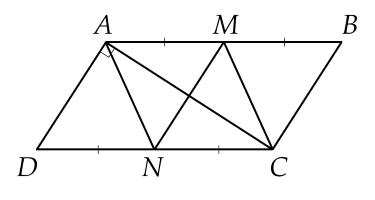
ABCD là hình bình hành nên AB//CD và AB = CD
Mà AM = 1/2 AB, DN = NC = 1/2 DC \(\Rightarrow AM=DN=NC\)
Do đó: AMCN và AMND là hình bình hành
MN // AD (cmt)
Kết hợp với \(AD\perp AC\left(gt\right)\Rightarrow MN\perp AC\)(1)
Mặt khác, AMCN là hình bình hành (2)
Từ (1) và (2), ta được AMCN là hình thoi.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: ABCDlà hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC
AMCN là hình bình hành
nên AC cắt MN tại trung điểm của mỗi đường
=>M đối xứng N qua O
Xét hbh ABCD có AB =CD;AB//CD
+) M,N lần lượt là trung điểm của AB,CD
=>AM=CN
+)M,N lần lượt là nằm trên của .AB,CD
=> AM//CN
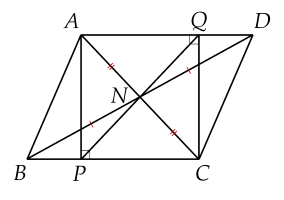
a) ����ABCD là hình bình hành nên ��=��AB=DC suy ra 12��=12��21AB=21DC
Do đó ��=��=��=��AM=BM=DN=CN.
Tứ giác ����AMCN có ��AM // ��,��=��NC,AM=NC nên là hình bình hành.
Lại có Δ���ΔADC vuông tại �A có ��AN là đường trung tuyến nên ��=12��=��=��AN=21DC=DN=CN.
Hình bình hành ����AMCN có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo ��,��AC,MN vuông góc với nhau.
Tứ giác ����AMCN là hình thoi.