
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có, mai mình thi cấp trường IOE, chúc NGÔ HỒNG PHÚC thi tốt nhé, chỉ cần qua 1500đ là ok ùi ^^
ngày mai mình thi học kì, đây là bài luyện tập, các bạn làm hộ để mình check bài với ạ. cảm ơn nhiều 

\(a,ĐK:x\ne0;x\ne5\\ B=\dfrac{x^2-25+2x^2-12x-x^2+8x+25}{2x\left(x-5\right)}=\dfrac{2x\left(x-2\right)}{2x\left(x-5\right)}=\dfrac{x-2}{x-5}\\ b,x=3\Leftrightarrow A=\dfrac{3+6}{5-3}=\dfrac{9}{2}\\ c,\text{Câu a}\\ d,E=B-A=\dfrac{x-2}{x-5}+\dfrac{x+6}{x-5}=\dfrac{2x+4}{x-5}=\dfrac{2\left(x-5\right)+14}{x-5}=2+\dfrac{14}{x-5}\in Z\\ \Leftrightarrow x-5\inƯ\left(14\right)=\left\{-14;-7;-2;-1;1;2;7;14\right\}\\ \Leftrightarrow x\in\left\{-9;-2;3;4;6;7;12;19\right\}\)

à hì hì
chúc shin thi tốt lun nha
sau này sẽ có cơ hội gặp mặt

1) \(=\left(9x^2-25y^2\right)-\left(6x-10y\right)=\left(3x-5y\right)\left(3x+5y\right)-2\left(3x-5y\right)=\left(3x-5y\right)\left(3x+5y-2\right)\)
2) \(=9x^2y^2-\left(x^2-2xy+y^2\right)=9x^2y^2-\left(x-y\right)^2=\left(3xy-x+y\right)\left(3xy+x-y\right)\)

Lời giải:
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+6x+6y+y^2+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+y^2+8=0$
$\Leftrightarrow (x+y+3)^2+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
Vậy $P_{\min}=2020; P_{\max}=2022$
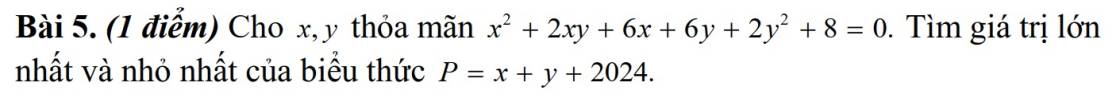 cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h
cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h
Chúc thi tốt!!!!!!Có j ko biết thì tài liệu
Cố lên!!!!!