Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)
Li độ cực đại kế tiếp cách nhau 1 chu kì dao động.
Như vậy, thời điểm kế tiếp li độ đạt cực đại là: \(t_2=0,2+0,5=0,7s\)

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Hướng dẫn: Chọn đáp án B
Tần số góc và chu kì:
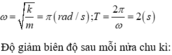
![]()
![]()

tức là biên độ so với I’ là

nên vật chưa vượt qua tâm dao động I’ nên tốc độ cực đại sau thời điểm 21,4 s chính là tốc độ qua I’ ở thời điểm
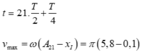
= 5 , 7 π cm / s
Bình luận: Tốc độ cực đại sau thời điểm t = 21 . T 2 + T 4 thì phải tính ở nửa chu kì tiếp theo:
![]()
![]()

Hướng dẫn: Chọn đáp án A
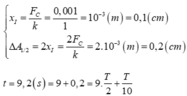
Lúc này vật qua VTCB 9 lần và đang chuyển động đến tâm dao động I’.
Li độ cực đại sau khi qua VTCB lần n = 9:
![]()
Tốc độ cực đại:
![]()
![]()
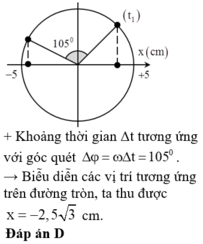
Chú ý: Để tìm li độ hoặc thời gian chuyển động ta phải xác định được tâm dao động tức thời và biên độ so với tâm dao động.

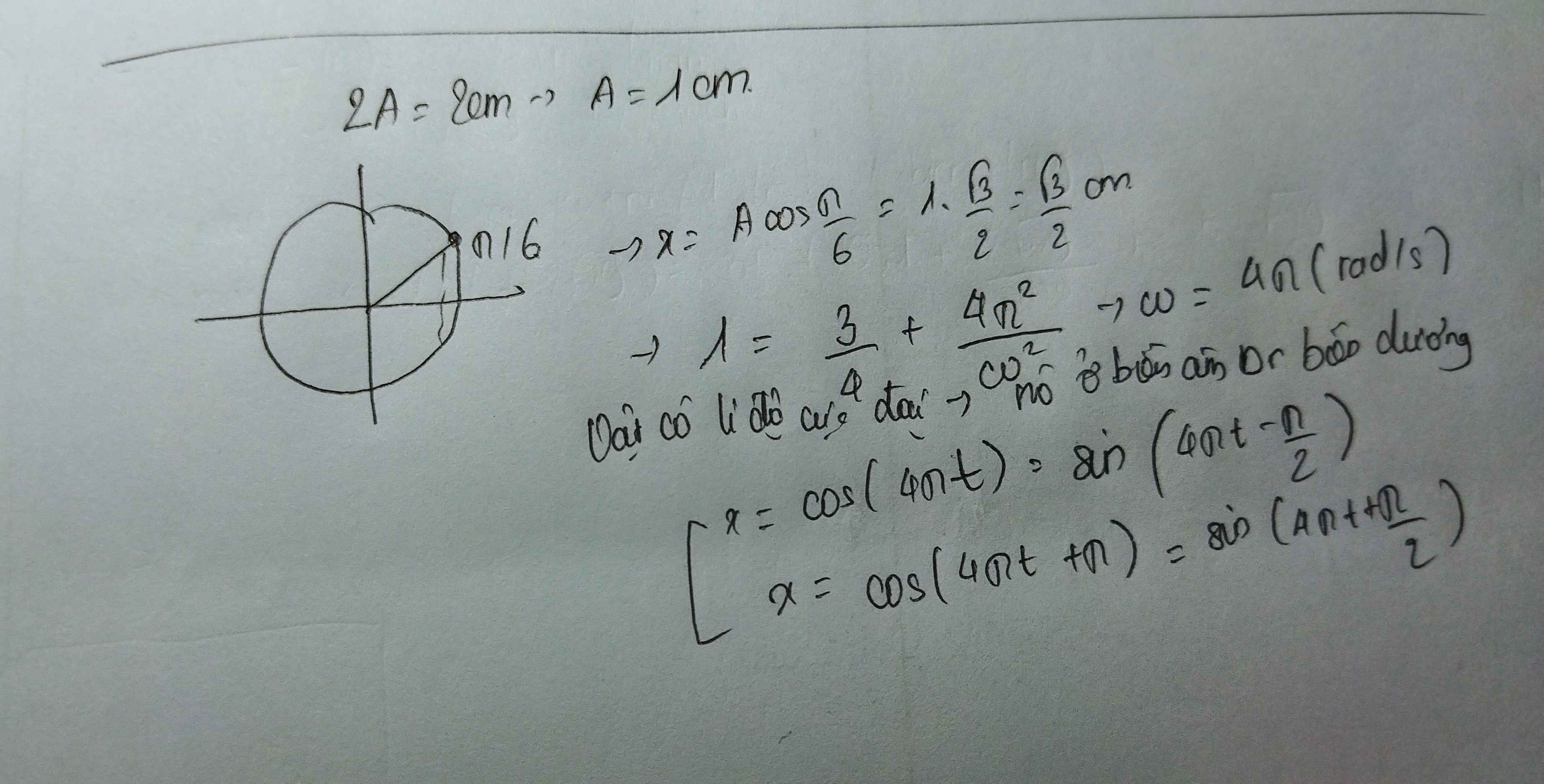
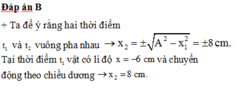
ALOSOALOSO