Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Đáp án A
Hai thời điểm vuông pha nhau, ta có A = x 1 2 + x 2 2 = 5

+ Không làm mất tính tổng quát có thê xem ở thời điểm t1, vật có vận tốc v0 và đang tăng, đến thời điểm t2 vật có vận tốc v0 và đang giảm, đến thời điểm t3 vật có vận tốc -v0 và đang giảm
+ Theo bài ra: t 3 − t 1 = 2 Δ t + 2 T 4 − Δ t t 3 − t 2 = 2 Δ t = 3.2 Δ t ⇒ Δ t = T 12 → t 3 − t 1 = 3 t 3 − t 2 2 Δ t + 2 T 4 − Δ t
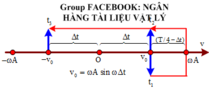
+ Thay Δ t = T 12 vào công thức v 0 = v max . sin 2 π T Δ t ta tính ra được v max = 40 c m / s
Chọn đáp án B




Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)
Li độ cực đại kế tiếp cách nhau 1 chu kì dao động.
Như vậy, thời điểm kế tiếp li độ đạt cực đại là: \(t_2=0,2+0,5=0,7s\)