OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

Tham gia chương tình "Học kỳ rực rỡ" cùng OLM cơ hội nhận quà lên tới 2.000.000Đ

Cơ hội nhận 15 ngày VIP dành cho thầy cô nhân dịp đầu năm

K
Khách

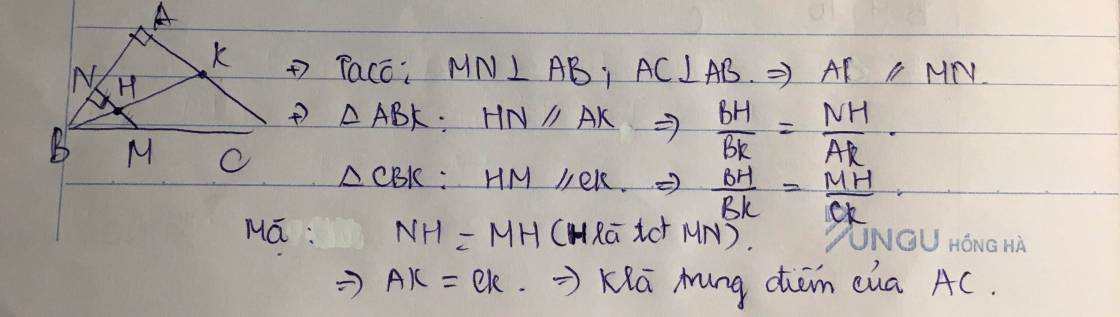
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
DP
Đào Phương Duyên
13 tháng 12 2016
1, Cho tam giác ABC , M, N lần lượt là trung điểm của AB , AC a, Tứ giác BMNC là hình gì ? b, Gọi I là trung điểm của MN , đường thẳng AI cắt BC tại K . Tứ giác AMKN là hình gì ? Vì sao ? c, Tam giác ABC cần điều kiện gì để AMKN là hình thoi . d, Vói điều kiện trên của tam giác ABC . Vẽ KH vuông góc với AC tại H . Đường thẳng KH cắt MN tại E . Chứng minh tam giác AME vuông 2, Cho tam giác ABC cân tai A...
Đọc tiếp

1, Cho tam giác ABC , M, N lần lượt là trung điểm của AB , AC

a, Tứ giác BMNC là hình gì ?

b, Gọi I là trung điểm của MN , đường thẳng AI cắt BC tại K . Tứ giác AMKN là hình gì ? Vì sao ?

c, Tam giác ABC cần điều kiện gì để AMKN là hình thoi .

d, Vói điều kiện trên của tam giác ABC . Vẽ KH vuông góc với AC tại H . Đường thẳng KH cắt MN tại E . Chứng minh tam giác AME vuông

2, Cho tam giác ABC cân tai A lấy điểm M trên cạnh AB . Từ M kẻ đường thẳng song song với AC cắt BC tại E

a, Chứng minh tam giác BME cân

b, Trên tia đối của tia CA lấy điểm N sao cho CN = BM . Tứ giác MCNE là hình gì ?

c, Gọi I là trung điểm của CE . Chứng minh M,N,I thẳng hàng

d, Từ M kẻ đường thẳng song song với BC cắt AC tại F . Từ N kẻ đường thẳng song song với BC cắt Me tại K . Chứng minh F,I,K thẳng hàng

 
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
5 tháng 3 2022

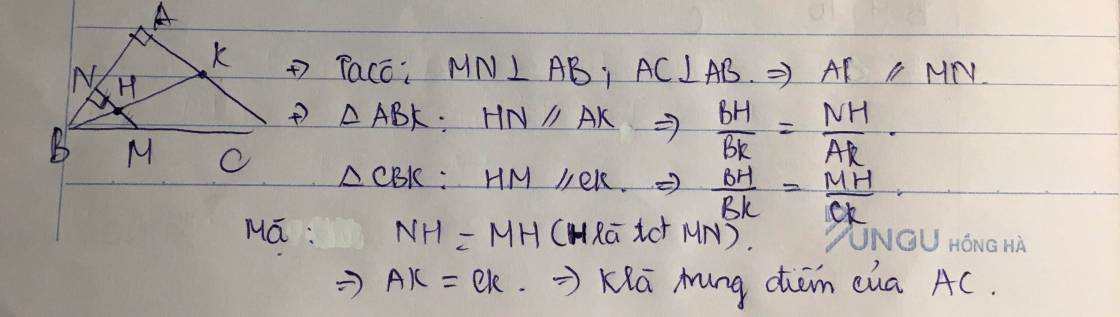
Bài 1: 

a: Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình

=>MN//BC

hay BMNC là hình thang

b: Xét ΔABK có MI//BK

nên MI/BK=AM/AB=1/2(1)

XétΔACK có NI//CK

nên NI/CK=AN/AC=1/2(2)

Từ (1)và (2) suy ra MI/BK=NI/CK

mà MI=NI

nên BK=CK

hay K là trug điểm của BC

Xét ΔABC có 

K là trung điểm của BC

M là trung điểm của AB

Do đó: KM là đường trung bình

=>KM//AN và KM=AN

hay AMKN là hình bình hành

Đúng(0)
PH
Phạm Hoài Thu Thảo
2 tháng 11 2018 - olm
Bài 1: Cho hình thang cân ABCD có AB // CD, AB = 4 cm, CD = 10 cm, AD = 5 cm. Trên tia đối của tia BD lấy điểm E sao cho BE = BD. Gọi H là chân đường vuông góc kẻ từ E đến BC. Tính độ dài CHBài 2: Cho tam giác ABC điểm D thuộc tia đối của tia BA sao cho BE = BA, M là trung điểm của BC, K là giao điểm của DM và AC. Chứng minh rằng AK = 2KCBài 3: Cho tam giác ABC, gọi M,N,P lần lượt là trung điểm của AB, AC, BC....
Đọc tiếp

Bài 1: Cho hình thang cân ABCD có AB // CD, AB = 4 cm, CD = 10 cm, AD = 5 cm. Trên tia đối của tia BD lấy điểm E sao cho BE = BD. Gọi H là chân đường vuông góc kẻ từ E đến BC. Tính độ dài CH

Bài 2: Cho tam giác ABC điểm D thuộc tia đối của tia BA sao cho BE = BA, M là trung điểm của BC, K là giao điểm của DM và AC. Chứng minh rằng AK = 2KC

Bài 3: Cho tam giác ABC, gọi M,N,P lần lượt là trung điểm của AB, AC, BC. Tính cho tam giác MNP, biết cạnh AB = 8 cm, AC = 10cm, BC = 12 cm
Giúp mình nhé, cảm ơn !
#Toán lớp 8
0
QA
Quynh Anh Quach
18 tháng 10 2015 - olm
Bài 1: Cho tam giác ABC vuông cân tại A, I là trung điểm BC, lấy H là điểm bất kì trên BC, kẻ HE vuông góc với AB, HF vuông góc với AC. Hỏi tam giác IEF là tam giác gì?Bài 2: Cho tam giác ABC, các đường cao AD, BE, CF cắt nhau tại H. I, K, R lần lượt là trung điểm HA, HB, HC. M, N, P lần lượt là trung điểm BC, AC, AB. a) CM MNIK, PNRK là hình chữ nhật. b) CM P,N,R,K,M,I cùng thuộc 1 đường tròn. c) CM 3 điểm D,...
Đọc tiếp

Bài 1: Cho tam giác ABC vuông cân tại A, I là trung điểm BC, lấy H là điểm bất kì trên BC, kẻ HE vuông góc với AB, HF vuông góc với AC. Hỏi tam giác IEF là tam giác gì?

Bài 2: Cho tam giác ABC, các đường cao AD, BE, CF cắt nhau tại H. I, K, R lần lượt là trung điểm HA, HB, HC. M, N, P lần lượt là trung điểm BC, AC, AB. a) CM MNIK, PNRK là hình chữ nhật. b) CM P,N,R,K,M,I cùng thuộc 1 đường tròn. c) CM 3 điểm D, E, F cũng thuộc đường tròn trên
#Toán lớp 8
0
PP
Pox Pox
29 tháng 11 2019 - olm
Cho tam giác ABC vuông tại B ( AB < BC ) , kẻ đường cao BH ( H thuộc AC ) . Lấy điểm M đối xứng với H qua BC , HM cắt BC tại I . Kẻ HK // BC ( K thuộc BC )a) Tứ giác BKHI là hình gì ? Vì sao ?b) Qua M kẻ đường thẳng MN // BH ( N thuộc BC ) . Chứng minh BMHN là hình thoic) Tính BH biết AB = 6cm , diện tích tam giác là \(24cm^2\)d) Tìm điều kiện để tam giác ABC để hình thoi BMHN là hình...
Đọc tiếp

Cho tam giác ABC vuông tại B ( AB < BC ) , kẻ đường cao BH ( H thuộc AC ) . Lấy điểm M đối xứng với H qua BC , HM cắt BC tại I . Kẻ HK // BC ( K thuộc BC )

a) Tứ giác BKHI là hình gì ? Vì sao ?

b) Qua M kẻ đường thẳng MN // BH ( N thuộc BC ) . Chứng minh BMHN là hình thoi

c) Tính BH biết AB = 6cm , diện tích tam giác là \(24cm^2\)

d) Tìm điều kiện để tam giác ABC để hình thoi BMHN là hình vuông
#Toán lớp 8
0
NT
Nguyễn Thị Bình
15 tháng 1 2017 - olm
Cho tam giác ABC vuông tại A có AB<AC. Gọi M,N và E lần lượt là trung điểm của AB,AC và BC. Trên tia đối của tia NB lấy D sao cho N là trung điểm BDa) Với AB=12cm, AC=16cm Tính dộ dài BC và MNb) Chứng minh tứ giác ABCD là hình bình hànhc) Trên tia đối của tia EA lấy K sao cho E là trung điểm của AK. Chứng minh tứ giác ABKC là hình chữ nhậtd) TRên AD lấy điểm F sao cho AF=FC. Chứng minh tứ giác AFCE là hình...
Đọc tiếp

Cho tam giác ABC vuông tại A có AB<AC. Gọi M,N và E lần lượt là trung điểm của AB,AC và BC. Trên tia đối của tia NB lấy D sao cho N là trung điểm BD

a) Với AB=12cm, AC=16cm Tính dộ dài BC và MN
b) Chứng minh tứ giác ABCD là hình bình hành
c) Trên tia đối của tia EA lấy K sao cho E là trung điểm của AK. Chứng minh tứ giác ABKC là hình chữ nhật
d) TRên AD lấy điểm F sao cho AF=FC. Chứng minh tứ giác AFCE là hình thoi
e) Từ B vẽ đường thẳng vuông góc với BC cắt đường thẳng CA tại I. Trên tia đối của tia IB lấy điểm H sao cho I là trung điểm của BH. Chứng minh HA vuông góc với BN
CÁC BẠN CHỈ CẦN LÀM PHẦN D VỚI E HỘ MÌNH THÔI ;; ;; HAI PHẦN NÀY KHÓ QUÁ .. HELP ME,pls !! 
#Toán lớp 8
0
NT
Nguyễn Thị Bình
15 tháng 1 2017 - olm
Cho tam giác ABC vuông tại A có AB<AC. Gọi M,N và E lần lượt là trung điểm của AB,AC và BC. Trên tia đối của tia NB lấy D sao cho N là trung điểm BDa) Với AB=12cm, AC=16cm Tính dộ dài BC và MNb) Chứng minh tứ giác ABCD là hình bình hànhc) Trên tia đối của tia EA lấy K sao cho E là trung điểm của AK. Chứng minh tứ giác ABKC là hình chữ nhậtd) TRên AD lấy điểm F sao cho AF=FC. Chứng minh tứ giác AFCE là hình...
Đọc tiếp

Cho tam giác ABC vuông tại A có AB<AC. Gọi M,N và E lần lượt là trung điểm của AB,AC và BC. Trên tia đối của tia NB lấy D sao cho N là trung điểm BD

a) Với AB=12cm, AC=16cm Tính dộ dài BC và MN
b) Chứng minh tứ giác ABCD là hình bình hành
c) Trên tia đối của tia EA lấy K sao cho E là trung điểm của AK. Chứng minh tứ giác ABKC là hình chữ nhật
d) TRên AD lấy điểm F sao cho AF=FC. Chứng minh tứ giác AFCE là hình thoi
e) Từ B vẽ đường thẳng vuông góc với BC cắt đường thẳng CA tại I. Trên tia đối của tia IB lấy điểm H sao cho I là trung điểm của BH. Chứng minh HA vuông góc với BN
CÁC BẠN CHỈ CẦN LÀM PHẦN D VỚI E HỘ MÌNH THÔI ;; ;; HAI PHẦN NÀY KHÓ QUÁ .. HELP ME,pls !!!!!!
#Toán lớp 8
0
D8
danh.05 8E
27 tháng 4 2022

Cho tam giác ABC vuông tại A có AB=6cm;BC=10cm. Trên canh BC lấy điểm M sao cho BM=18 cm từ điểm M kẻ đường thẳng vuông góc với BC cắt đường thẳng AB AC lần lược là N và P .cm tam giác ABC=tam giác MBN tính độ dài BN ,B/PA.PC=PM.PN
#Toán lớp 8
1
DT
Đỗ Thị Minh Ngọc
27 tháng 4 2022

 

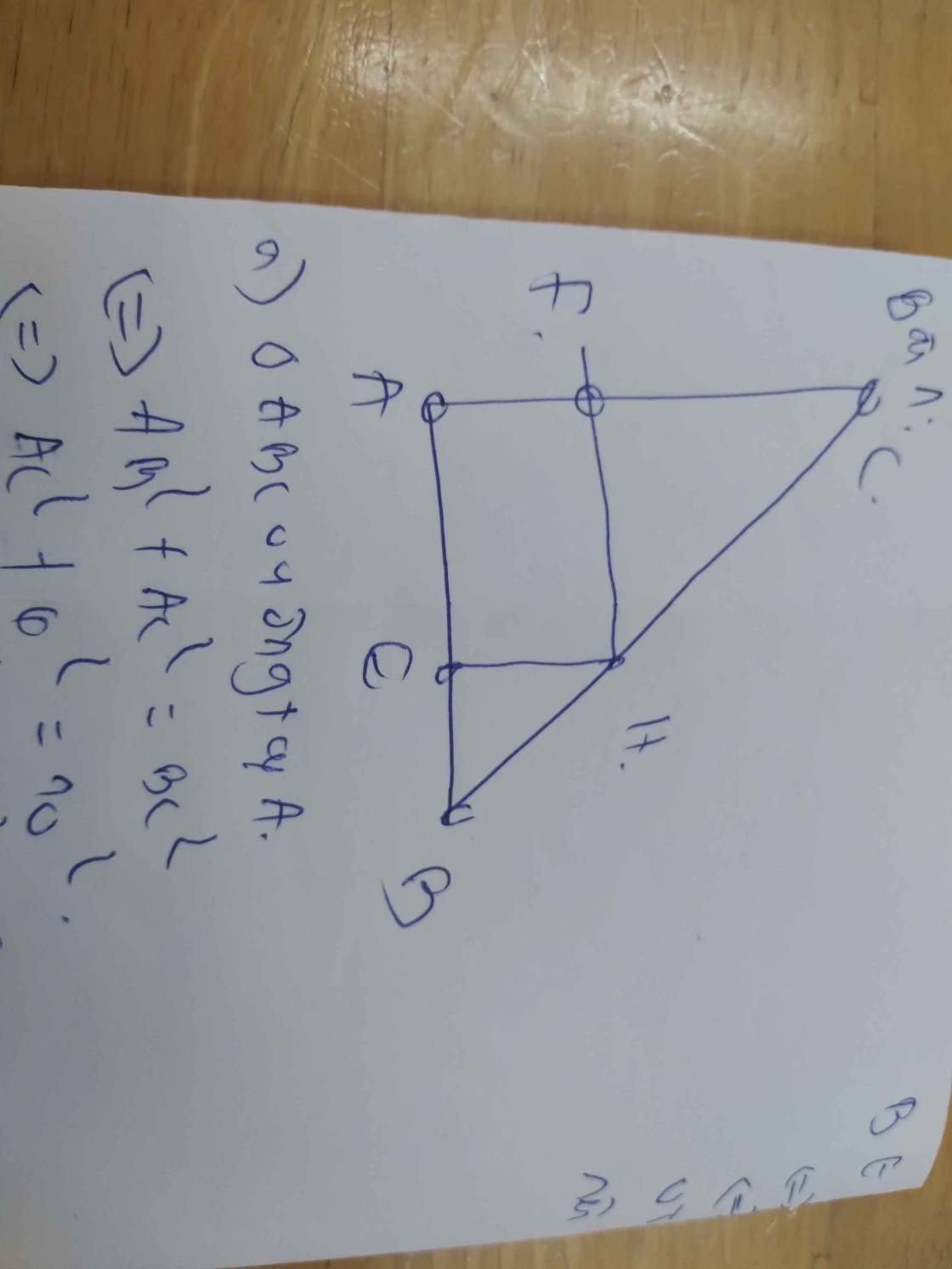
a)

Xét tam giác BAC vuông tại A và tam giác BMN vuông tại M có:

\(\widehat{BAC}\)=\(\widehat{BMN}\)

=> Tam giác BAC ᔕ  Tam giác BMN (g-g)

=> BA/BM=BC/BN

=> BN=BM.\(\dfrac{BC}{BA}\)=18.\(\dfrac{20}{12}\)=30cm

b)

Xét tam giác PAN vuông tại A và tam giác PMC vuông tại M có

\(\widehat{APN}\)=\(\widehat{MPC}\) (đối đỉnh)

=> Tam giác PAN ᔕ Tam giác PMC (g-g)

=> \(\dfrac{PA}{PM}\)=\(\dfrac{PN}{PC}\)

=> PA.PC=PM.PN (đpcm)

Đúng(1)
D
duongnhatninh
4 tháng 1 2015 - olm

Cho tam giác ABC vuông tại A, biết AB=6cm ,AC=8cm. Gọi M là trung điểm của đoạn thẳng BC

a, Tính độ dài BC,AM

b, Kẻ MDvuong góc AB (Dthuoc AB) ME vuông góc AC ( E thuoc AC) . Tứ giác ADME là hình gì?

c, Tam giác ABC có đk gì để tứ giác ADME là hình vuông ?

d, Gọi F đx với A qua M . Kể FH vuông góc vs BC ( H thuộc BC ) Gọi K là trung điểm của BH. CM : FK vuông góc vs EK ?
#Toán lớp 8
0
PH
PINK HELLO KITTY
4 tháng 1 2018 - olm

Cho tam giác ABC cân tại A. Gọi H, K lần lượt là trung điểm của BC, AC.

a) Chứng minh tứ giác ABHK là hình thang.

b) Qua A vẽ đường thẳng vuông góc với AH, cắt tia HK tại D. Chứng minh AD=BH.

c) Vẽ HN vuông góc với AB (N thuộc AB), gọi I là trung điểm của AN. Trên tia đối của tia BH, lấy điểm M sao cho B là trung điểm của HM. Chứng minh MN vuông góc với HI.
#Toán lớp 8
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP