Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b.
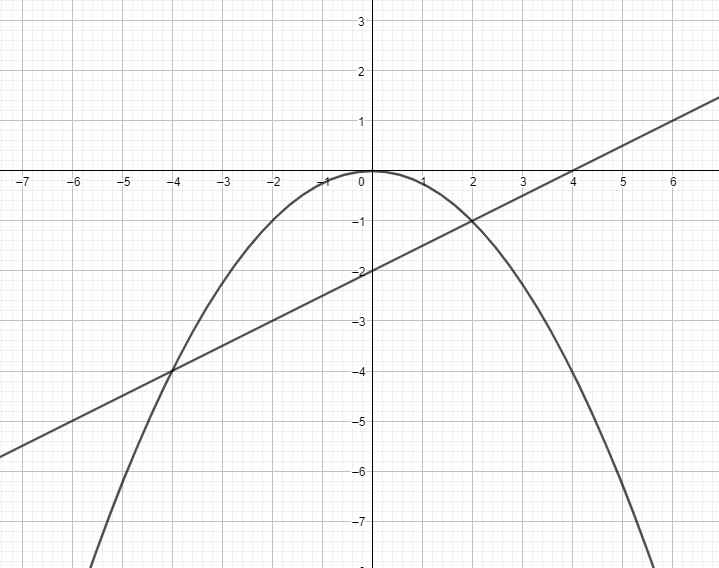
Phương trình hoành độ giao điểm (P) và (d):
\(-\dfrac{1}{4}x^2=\dfrac{1}{2}x-2\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow1=-1\\x=-4\Rightarrow y=-4\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là (2;-1) là (-4;-4)

a) \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}.\left(\sqrt{x}-1\right)=\dfrac{x-1}{\sqrt{x}}\)
b) \(A=2\Rightarrow\dfrac{x-1}{\sqrt{x}}=2\Rightarrow x-1=2\sqrt{x}\Rightarrow x-2\sqrt{x}-1=0\)
\(\Rightarrow x-2\sqrt{x}+1=2\Rightarrow\left(\sqrt{x}-1\right)^2=2\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=\sqrt{2}\\\sqrt{x}-1=-\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=\sqrt{2}+1\\\sqrt{x}=1-\sqrt{2}\left(l\right)\end{matrix}\right.\Rightarrow x=\left(\sqrt{2}+1\right)^2=3+2\sqrt{2}\)
c) \(A< 0\Rightarrow\dfrac{x-1}{\sqrt{x}}< 0\) mà \(\sqrt{x}>0\Rightarrow x-1< 0\Rightarrow x< 1\Rightarrow0< x< 1\)

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔEBD vuông tại E
Xét ΔBDA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)

a: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

Bài 2:
a) Ta có: \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{5}-\sqrt{2}}+\dfrac{6}{2-\sqrt{10}}-\dfrac{20}{\sqrt{10}}\)
\(=\dfrac{\sqrt{10}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{5}-\sqrt{2}}+\dfrac{6\cdot\left(\sqrt{10}+2\right)}{\left(\sqrt{10}-2\right)\left(\sqrt{10}+2\right)}-\dfrac{\sqrt{10}\cdot2\sqrt{10}}{\sqrt{10}}\)
\(=\sqrt{10}+\sqrt{10}-2-2\sqrt{10}\)
=-2
b) Ta có: \(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
\(=\left(\sqrt{5}-1-2\right)\left(\sqrt{5}-1+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)\)
=5-9=-4
c) Ta có: \(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\dfrac{\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}\)
\(=\dfrac{8-2\sqrt{15}+8+2\sqrt{15}}{2}-\dfrac{6+2\sqrt{5}}{4}\)
\(=\dfrac{16}{2}-\dfrac{6+2\sqrt{5}}{4}\)
\(=\dfrac{32-6-2\sqrt{5}}{4}\)
\(=\dfrac{26-2\sqrt{5}}{4}\)
\(=\dfrac{13-\sqrt{5}}{2}\)

Bài 9:
Ta có: \(a-4+\sqrt{16-8a+a^2}\)
\(=a-4+\sqrt{\left(a-4\right)^2}\)
\(=a-4+a-4\)
=2a-8
a)\(\dfrac{x^2-3}{x^2+2x\sqrt{3}+3}=\dfrac{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}{\left(x+\sqrt{3}\right)^2}=\dfrac{x-\sqrt{3}}{x+\sqrt{3}}\)
\(\dfrac{x^2-2x\sqrt{15}+15}{x^2-15}=\dfrac{\left(x-\sqrt{15}\right)^2}{\left(x-\sqrt{15}\right)\left(x+\sqrt{15}\right)}=\dfrac{x-\sqrt{15}}{x+\sqrt{15}}\)
\(\dfrac{4x^2-6}{4x^2-4x\sqrt{6}+6}=\dfrac{\left(2x-\sqrt{6}\right)\left(2x+\sqrt{6}\right)}{\left(2x-\sqrt{6}\right)^2}=\dfrac{2x+\sqrt{6}}{2x-\sqrt{6}}\)
b) \(\dfrac{a^2+2a\sqrt{8}+8}{a^2-8}=\dfrac{\left(a+\sqrt{8}\right)^2}{\left(a+\sqrt{8}\right)\left(a-\sqrt{8}\right)}=\dfrac{a+\sqrt{8}}{a-\sqrt{8}}\)
\(\dfrac{9x^2-15}{9x^2-6x\sqrt{15}+15}=\dfrac{\left(3x-\sqrt{15}\right)\left(3x+\sqrt{15}\right)}{\left(3x-\sqrt{15}\right)^2}=\dfrac{3x+\sqrt{15}}{3x-\sqrt{15}}\)
\(\dfrac{a^2-2a\sqrt{7}+7}{a^2-7}=\dfrac{\left(a-\sqrt{7}\right)^2}{\left(a-\sqrt{7}\right)\left(a+\sqrt{7}\right)}=\dfrac{a-\sqrt{7}}{a+\sqrt{7}}\)

1:
Khi x=36 thì \(A=\dfrac{6+4}{6-4}=\dfrac{10}{2}=5\)
2: \(B=\dfrac{3\sqrt{x}-12+16-2\sqrt{x}}{x-16}=\dfrac{\sqrt{x}+4}{x-16}=\dfrac{1}{\sqrt{x}-4}\)
3: A=B*|x-2|
=>|x-2|=A/B=căn x+4
=>x-2=căn x+4 hoặc x-2=-căn x-4
=>x-căn x-6=0 hoặc x+căn x+2=0
=>x=9


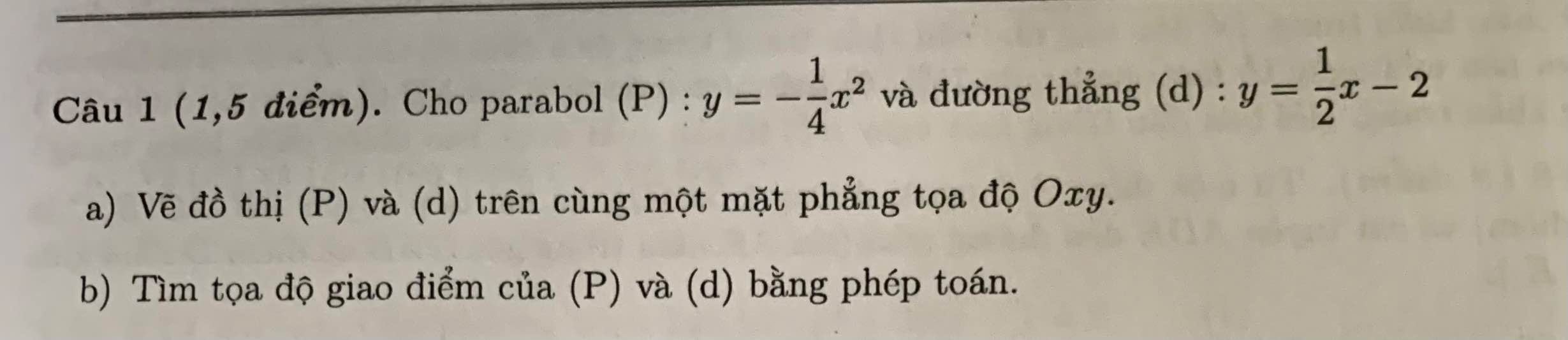

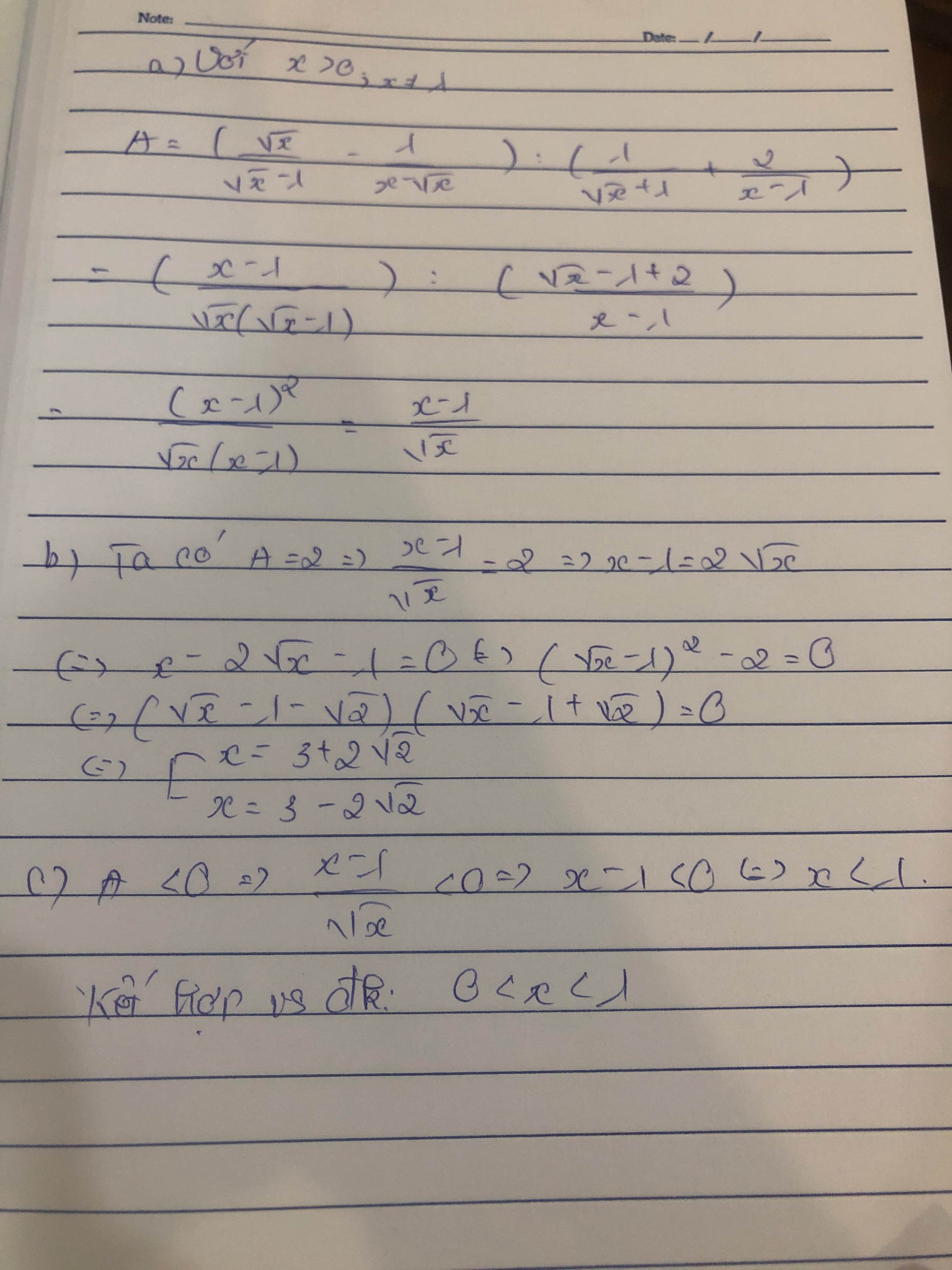



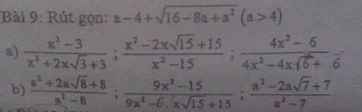


cái nằm trên đầu 3x+1 và 2+x là gì vậy
giá trị tuyệt đối