


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





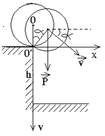
Hệ vật ta xét gồm "Quả cầu - Lò xo - Trái Đất" là hệ cô lập.
Cơ năng W của hệ vật này có giá trị bằng tổng của động năng ( W đ ), thế năng trọng trường ( W t ) và thế năng đàn hồi ( W đ h ) :
W = W đ + W t + W đ h
Chọn gốc toạ độ là vị trí cân bằng của hệ vật (quả cầu đứng yên) và chiều dương là chiều lò xo bị kéo dãn. Do đó ta có :
- Tại vị trí ban đầu : hệ vật có W đ = 0 ( v 0 = 0) lò xo bị dãn một đoạn Δ so với vị trí cân bằng, nên W t ≠ 0, W đ h ≠ 0 và cơ năng của hệ vật bằng :
W 0 = 0 + mg ∆ l + k ∆ l + ∆ l 0 2 /2
- Khi về tới vị trí cân bằng : quả cầu có W đ ≠ 0 (v ≠ 0) và W t = 0 (trùng với gốc tính thế năng đàn hồi), đồng thời lò xo bị dãn một đoạn Δ0, nên cơ năng của hệ vật bằng :
W = m v 2 /2 + 0 + k ∆ l 0 2 /2
Chú ý : Hệ vật này được treo thẳng đứng nên tại vị trí cân bằng của nó, lò xo đã bị dãn một đoạn ∆ 0 thoả mãn điều kiện :
mg + k ∆ 0 = 0 ⇒ mg = -k ∆ 0
với P = mg là trọng lực và F đ h = k ∆ là lực đàn hồi tác dụng lên hệ vật
Áp dụng định luật bảo toàn cơ năng cho hệ vật, ta có :
W = W 0 ⇒ mg ∆ l + k ∆ l + ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
⇒ mg ∆ l + k ∆ l 2 /2 + k ∆ l ∆ l 0 /2 + k ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
Vì mg = -k ∆ 0 , nên sau khi rút gọn hai vế của phương trình, ta được
k ∆ l 2 /2 = m v 2 /2
Từ đó suy ra vận tốc của quả cầu khi nó về tới vị trí cân bằng:
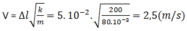

a) Chọn gốc thế năng trọng trường tại C ( Hình 92).
Theo định luật bảo toàn cơ năng: W A = W M
![]()
Vận tốc của m tại một điểm trên quỹ đạo ( ứng với góc lệch α )
![]()
Vận tốc v sẽ đạt cực đại khi cos α = 1 hay α = 0 .
![]()
b) Phương trình chuyển động của m: P → + T → = m a →
Chiếu phương trình lên phương bán kính đi qua M, chiều dương hướng vào điểm treo:
![]()
Thay ![]() vào phương trình của T ta được:
vào phương trình của T ta được:
Lực căng dây tại M ( ứng với góc lệch: T = m g 3 cos α - 2 cos α 0
Lực căng T đạt cực đại khi cos α = 1 hay α = 0 : T = m g 3 - 2 cos α 0

a/ Chọn gốc toạ độ là mặt đất, chiều dương hướng lên trên, thời gian tính từ lúc quả cầu thứ nhất xuất phát
Xét vật 1: \(\left\{{}\begin{matrix}v_0=20m/s\\a=-10m/s\\t_0=0\end{matrix}\right.\)
\(\Rightarrow x_1=v_0t+\frac{1}{2}at^2=20t-\frac{1}{2}.10.t^2=20t-5t^2\)
Xét vật 2: \(\left\{{}\begin{matrix}a_2=-10m/s\\x_0=35m\\t_0=1s\end{matrix}\right.\)
\(\Rightarrow x_2=x_0+v_0t+\frac{1}{2}at^2=35-\frac{1}{2}.10.\left(t-1\right)^2=35-5\left(t-1\right)^2\)
Hai quả cầu ở cùng độ cao nghĩa là chúng gặp nhau<=> x1= x2
\(\Leftrightarrow20t-5t^2=30-5t^2+10t\)
\(\Leftrightarrow t=3s\) tại độ cao 15m
Phương trình vận tốc của quả cầu 1:
v1 = v0 – gt = 20 – 10t
Lúc t = 3s, v1 = -10m/s
Vậy lúc hai quả cầu ở cùng độ cao, quả cầu 1 đang đi xuống với vận tốc 10 m/s
b/ Cách nhau 10m nghĩa là |x1-x2|= 10 cậu tự gỉai
c/ 2 quả cầu chuyển động ngc chiều thì dĩ nhiên chúng phải gặp nhau=> k/c ngắn nhất =0
d/ Quả cầu 1 ở độ cao cực đại tức là v1= 0
<=> 20-10t= 0
<=> t= 2(s)
Thay vào từng ptcđ của từng vật rồi trừ đi là ra( lazy =))

Chọn hệ quy chiếu với gốc tọa độ là vị trí ban đầu, trục Oy hướng xuống dưới, trục Ox trùng hướng với vecto vận tốc ban đầu. Gốc thời gian tại lúc ném
Thời gian quả cầu rơi là:
$t = \sqrt{\dfrac{2H}{g}} = \sqrt{\dfrac{2.80}{10}} = 4 (s)$
Vận tốc của quả cầu lúc chạm đất là:
$v = \sqrt{v_0^2 + 2gH} = \sqrt{20^2 + 2.10.80} = 20\sqrt{5} (m/s)$.

Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)