K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2021
b) \(\left(x+1\right)^2=2\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)^2-2\left(x+1\right)+1=1\)
\(\Leftrightarrow\left(x+1-1\right)^2=1\)
\(\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
KV
8 tháng 11 2023
16 ⋮ (x - 1)
⇒ x - 1 ∈ Ư(16) = {-16; -8; -4; -2; -1; 1; 2; 4; 8; 16}
⇒ x ∈ {-15; 17; -3; -1; 0; 2; 3; 5; 9; 17}
Mà x ≤ 10
⇒ x ∈ {-15; 17; -3; -1; 0; 2; 3; 5; 9}
(Nếu đề yêu cầu x là số tự nhiên thì: x ∈ {0; 2; 3; 5; 9})
27 tháng 6 2023
2:
a: =>1/3x=16+1/4-13-1/4=3
=>x=9
b: =>4,5-2x=11/14:(-11/7)=-1/2=-0,5
=>2x=5
=>x=2,5
3:
Số học sinh giỏi là 12*5/6=10 bạn
Số học sinh trung bình là 10*1,4=14 bạn
Số học sinh của lớp là 10+12+14=36 bạn
D
1
10 tháng 10 2023
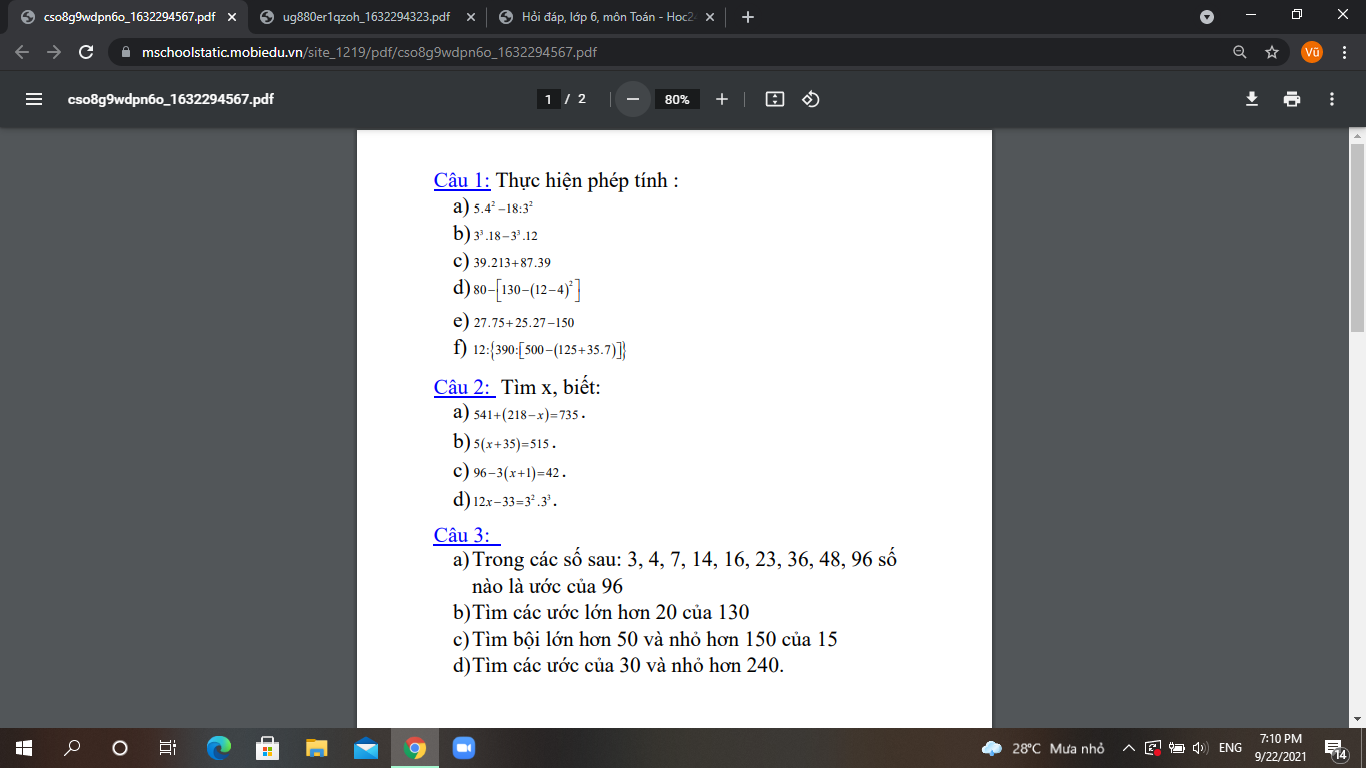
Bài 1.
a,Vì \(\dfrac{a}{b}>1\)=>a<b
Với m∈N* Ta có
\(am> bm\)=>\(am+ab> bm+ab\)=>\(a\left(b+m\right)> b\left(a+m\right)\)=>\(\dfrac{a}{b}>\dfrac{a+m}{b+m} \)
b, Vì \(\dfrac{a}{b}< 1\)=>a<b
Với m∈N* =>
\(am< bm\)=>\(am+ab< bm+ab\)=>\(a\left(b+m\right)< b\left(a+m\right)\)=>\(\dfrac{a}{b}<\dfrac{a+m}{b+m} \)
Tự áp dụng cho bài 2 nhé bạn :)
NH
7
NT
1
AH
Akai Haruma
Giáo viên
30 tháng 7 2023
Lời giải:
$(x-15)-x.13=0$
$x-15-x.13=0$
$(x-x.13)-15=0$
$x(1-13)-15=0$
$x.(-12)-15=0$
$x.(-12)=15$
$x=15:(-12)=\frac{-5}{4}$
8 tháng 1 2022
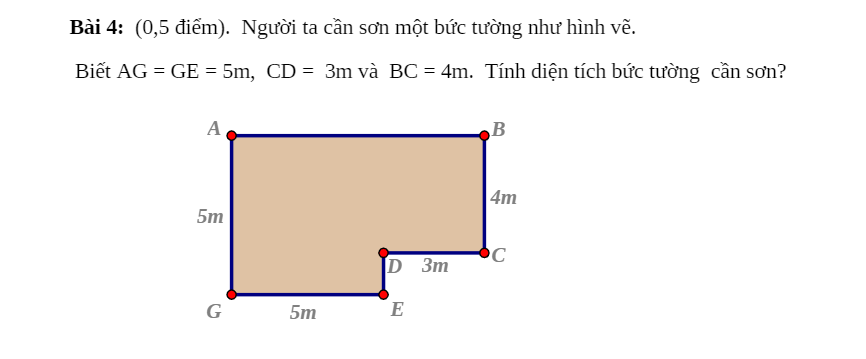
Ta chia ra thành 2 hình như sau:
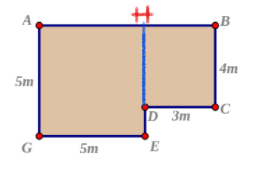
S HBCD là : 3 x 4 = 12 ( m2)
S AHEG là : 5 x 5 = 25 ( m2)
S bức tường cần sơn là : 12 + 25 = 37( m2)
Đ/s : 37 m2
5 tháng 5 2021
Ta có \(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{49.51}\)
=\(\dfrac{2}{2}\).(\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{49.51}\))
=\(\dfrac{1}{2}\).(\(\dfrac{2}{1.3}\)+\(\dfrac{2}{3.5}\)+\(\dfrac{2}{5.7}\)+...+\(\dfrac{2}{49.50}\))
=\(\dfrac{1}{2}\).(1-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\))
=\(\dfrac{1}{2}\).(\(1-\dfrac{1}{51}\))
=\(\dfrac{1}{2}\).\(\dfrac{50}{51}\)
=\(\dfrac{25}{51}\)
5 tháng 5 2021
Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{49\cdot51}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{49\cdot51}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{50}{51}=\dfrac{25}{51}\)