PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LV
3 tháng 4 2017
Lời giải:
Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
2.Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)
PT
1
CM
22 tháng 12 2017
+ Phương pháp nguyên hàm từng phần:
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x).v(x) - ∫v(x).u’(x)dx
Hay viết gọn: ∫udv = uv - ∫vdv.
CV
0
NV
13 tháng 1 2022
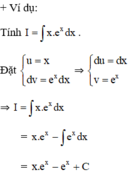
Thế nào là mẫu thống kê? Trình bày các cách thu gọn mẫu Lấy ví dụ minh hoạ và thu gọn mẫu đó theo các cách khác nhau?
H9
HT.Phong (9A5)
CTVHS
14 tháng 2 2023
Trong nghiên cứu thống kê và phương pháp nghiên cứu định lượng, một mẫu dữ liệu là một tập hợp các dữ liệu thu thập được và/ hoặc được lựa chọn từ một tổng thể thống kê bằng một quy tắc rõ ràng. ... Các mẫu được thu thập và thống kê được tính toán từ các mẫu để có thể kết luận hoặc ngoại suy từ các mẫu đến tổng thể.
Các tính chất :