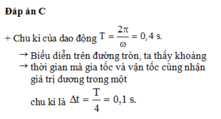Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Chu kì của dao động T = 2 π ω = 0 , 4 s
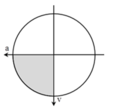
→ Biểu diễn trên đường tròn, ta thấy khoảng thời gian mà gia tốc và vận tốc cùng nhận giá trị dương trong một chu kì là Δt = T 4 = 0 , 1 s

Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác để xác định thời gian
Cách giải:
PT dao động x = 8cos(4πt + π/2) cm => Chu kì dao động T = 0,5s
Vận tốc và li độ cùng nhận giá trị dương <=> vật có li độ dương và vật chuyển động theo chiều dương
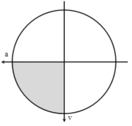
Biểu diễn trên đường tròn lượng giác ta có:
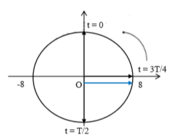
=> T/2 < t < 3T/4 => 0,25s < t < 0,375s.
=> Chọn B

Đáp án C

Vận tốc cực đại của dao động a m a x = ω A = 4 π cm / s
Tại thời điểm t = 0,25 s vật có vận tốc v = 2 2 x m a x = 2 π 2 cm / s
Tại thời điểm t=0 ứng với góc lùi ∆ φ = ω ∆ t = 0 , 25 π
Biễu diễn các vị trí tương ứng trên đường tròn. Ta thu được φ 0 = - π 2 r a d
Phương trình dao động của vật là x = 4 cos ( πt - π 2 ) c m

Vận tốc dương khi vật chuyển động theo chiều dương trục toạ độ.
Gia tốc có hướng về VT cân bằng, nên để gia tốc dương thì vật đi từ biên độ âm về VTCB.
Do vậy, vận tốc và gia tốc đều có giá trị dương khi vật đi từ biên độ âm về VTCB.
Thời gian ngắn nhất là 1/4 T.

Đáp án A
Phương pháp: a = - ω2x
Cách giải:
x (t=0,25s) = 1cm => a = - ω2x = - 40cm/s2

Đáp án A
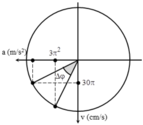
+ Biểu diễn các vị trí tương ứng trên đường tròn. Để thõa mãn điều kiện bài toán thì khoảng thời 1 60 s gian tương ứng với góc quét Δφ
→ Từ hình vẽ, ta có:
arcos 30 π ωA − arsin 300 π 2 ω 2 A 360 0 T = arcos 30 π 6 ω − arsin 300 π 2 6 ω 2 ω = 1 60
→ Phương trình trên cho ta nghiệm ω = 31,6 rad/s → T = 0,2 s