Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác để xác định thời gian
Cách giải:
PT dao động x = 8cos(4πt + π/2) cm => Chu kì dao động T = 0,5s
Vận tốc và li độ cùng nhận giá trị dương <=> vật có li độ dương và vật chuyển động theo chiều dương
Biểu diễn trên đường tròn lượng giác ta có:
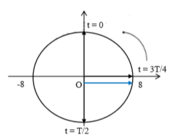
=> T/2 < t < 3T/4 => 0,25s < t < 0,375s.
=> Chọn B

+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s.
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad
+ Phương trình dao động của vật
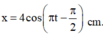
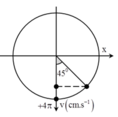
Đáp án C

Đáp án A
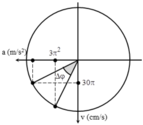
+ Biểu diễn các vị trí tương ứng trên đường tròn. Để thõa mãn điều kiện bài toán thì khoảng thời 1 60 s gian tương ứng với góc quét Δφ
→ Từ hình vẽ, ta có:
arcos 30 π ωA − arsin 300 π 2 ω 2 A 360 0 T = arcos 30 π 6 ω − arsin 300 π 2 6 ω 2 ω = 1 60
→ Phương trình trên cho ta nghiệm ω = 31,6 rad/s → T = 0,2 s

Chọn đáp án C
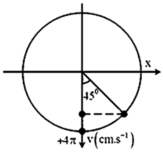
Vận tốc cực đại của dao động:
v max = ω A = 4 π c m / s .
Tại thời điểm t = 0,25 s vật có vận tốc:
v = 2 2 v max = 2 π 2 c m / s .
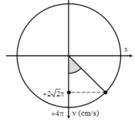
Biễu diễn các vị trí tương ứng trên đường tròn.
Ta thu được: φ 0 = − π 2 r a d .
Phương trình dao động của vật là:
x = 4 cos π t − π 2 c m .
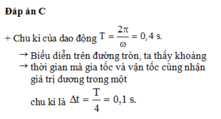
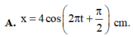
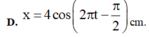





Đáp án C
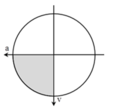
+ Chu kì của dao động T = 2 π ω = 0 , 4 s
→ Biểu diễn trên đường tròn, ta thấy khoảng thời gian mà gia tốc và vận tốc cùng nhận giá trị dương trong một chu kì là Δt = T 4 = 0 , 1 s