Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_{17}^5\)
a. Số cách chọn sao cho có đúng 3 nam (nghĩa là chọn 3 nam từ 9 nam và 2 nữ từ 8 nữ):
\(n_A=C_9^3.C_8^2\)
Xác suất: \(P_A=\dfrac{C_9^3.C_8^2}{C_{17}^5}=...\)
b. Chọn nhiều nhất 1 nữ nghĩa là ta có 2 TH có thể xảy ra: có 1 nữ và 4 nam hoặc cả 5 đều nam
Số cách chọn: \(n_B=C_8^1.C_4^9+C_9^5\)
Xác suất: \(P_B=\dfrac{C_8^1.C_9^4+C_9^5}{C_{17}^5}=...\)

a) Xác suất là 2/10 hoặc 1/5.
b) Xác suất là 3/10 hoặc 3/10. Giải bằng công thức hoặc bảng xác suất.

Số phân tử của không gian mẫu : \(n\left(\Omega\right)=C_{10}^2C_{10}^2=2970\)
Gọi các giáo viên được chọn có cả nam và nữ là : A
Suy ra A = Các giáo viên được chọn chỉ có nam và nữ
\(n\left(A\right)=C_3^2.C_3^2+C_7^2.C_9^2=765\)
\(n\left(A\right)=C_{10}^2.C_{12}^2-\left(C_3^2.C_3^2+C_7^2.C_9^2=2205\right)\)
\(P\left(A\right)=\frac{49}{66}\)
Đề thi khảo sát chất lượng lần 1- THPT Đức Thọ- Hà Tĩnh - Toán 12 - Đặng Ngọc Giáp - Thư viện Đề thi & Kiểm tra

Lời giải:
Số học sinh học ít nhất 1 môn toán là:
$36+16=52$ (hs)
Xác suất để sinh viên học ít nhất 1 môn toán: $\frac{52}{60}$

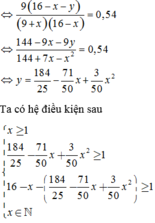
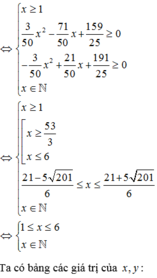



Đáp án A
Không gian mẫu là “Chọn ngẫu nhiên 2 người từ 10 học sinh trong tổ đó”. Suy ra số phần tử trong không gian mẫu là n ( Ω ) = C 10 2
Gọi A là biến cố “2 người được chọn là nữ” thì kết quả thuận lợi cho biến cố A là n ( A ) = C 3 2
Vậy xác suất cần tính là P ( A ) = n ( A ) n ( Ω ) = C 3 2 C 10 2 = 1 15 .