Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
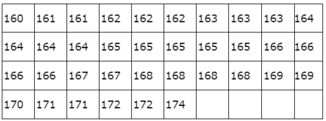
Khi đó chiều dài trung bình của 74 chiếc lá này là :


Số trung bình: \(\bar X = \frac{{48 + 53 + 51 + 31 + 53 + 112 + 52}}{7}\)\( = \frac{{400}}{7} \approx 57,14\)
Số trung vị:
Ta sắp xếp lại số liệu theo thứ tự không giảm:
31 48 51 52 53 53 112
Số giá trị là 7, là số lẻ nên giá trị chính giữa của mẫu là trung vị. Mà giá trị chính giữa là 52.
Vậy số trung vị là 52.
Ta thấy trong mẫu số liệu bài cho thì 112 cao hơn hẳn giá trị trung bình nên không thể dùng số trung bình để đại diện cho chiều dài của 7 con cá voi trưởng thành này.
Vậy ta dùng số trung vị để đại diện cho chiều dài của 7 con cá voi trưởng thành này.

Chọn A.
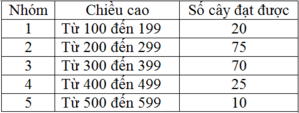
Từ bảng số liệu đã cho ta có bảng phân bố tần số; tần suất ghép lớn như sau:
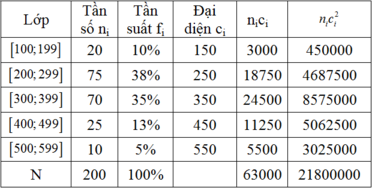
Dựa vào bảng trên ta có số trung bình cộng của dãy số liệu là:
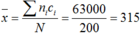

+) Gọi x là chiều dài của màn hình ti vi
y là chiều rộng của màn hình ti vi
+) Ta có hệ phương trình:
\( \Rightarrow \left\{ \begin{array}{l}{x^2} + {y^2} = {32^2}\\\frac{x}{y} = \frac{{16}}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \approx 27,890417\\y \approx 15,688359\end{array} \right.\) . Vậy chiều dài của ti vi là: 27,890417 (in)
+) Nếu lấy giá trị gần đúng của x là 27,89 thì: \(27,89 < x < 27,895\)
Suy ra: \(\left| {x - 27,89} \right| < 27,895 - 27,89 = 0,005\)
Vậy độ chính xác của số gần đúng là 0,005
+) Sai số tương đối của số gần đúng là: \(\delta = \frac{{0,005}}{{\left| {27,89} \right|}} = 0,018\% \)

Đáp án: D
Ta có sai số tuyệt đối của số đo chiều dài con dốc là :
Δa = a . δ a = 182,55. 0,2% = 0.3851.
Vì 0.05 < Δa < 0,5 . Do đó chữ số chắc của d là 1, 9, 2.
Vậy cách viết chuẩn của a là 193m (quy tròn đến hàng đơn vị).

Ta có bảng phân bố tần số ghép lớp sau:
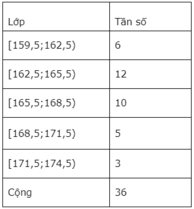
Từ đó ta thấy lớp L 2 có tần số cao nhất, do đó có tần suất cao nhất. Vì thế nó có diện tích lớn nhất. Đáp án là B.

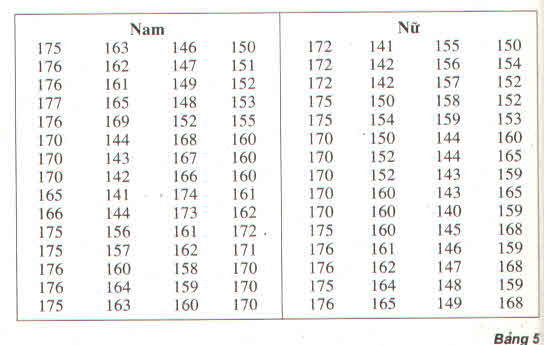
a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)

a) Số trung bình cộng của mẫu số liệu trên là: \(\overline X = \frac{{165 + 155 + 171 + 167 + 159 + 175 + 165 + 160 + 158}}{9} = 163,9\)
b) Mẫu số liệu theo thứ tự không giảm là:
155 158 159 160 165 165 167 171 175
Mẫu số liệu trên có 9 số liệu nên số trung vị là: \({M_e} = 165\)
c) Ta có bàng tần số
155 | 158 | 159 | 160 | 165 | 167 | 171 | 175 |
1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 |
Vậy mốt của mẫu số liệu là: \({M_o} = 165\)
d) Mẫu số liệu theo thứ tự không giảm là:
155 158 159 160 165 165 167 171 175
Mẫu số liệu trên có 9 số liệu nên số trung vị là: \({M_e} = 165\)
Trung vi của dãy số 155 158 159 160 là: \({Q_1} = \frac{{158 + 159}}{2} = 158,5\)
Trung vị của dãy số 165 167 171 175 là: \({Q_3} = \frac{{167 + 171}}{2} = 169\)
Vậy \({Q_1} = 158,5\), \({Q_2} = 165\), \({Q_3} = 169\)

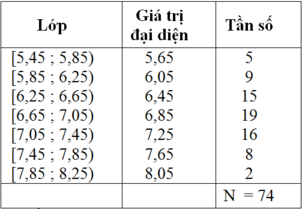
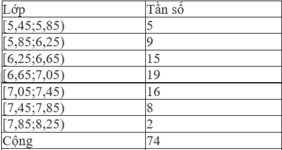
Ta bổ sung thêm một cột ghi giá trị đại diện của mỗi lớp:
Lớp |
Tần số |
Giá trị đại diện |
| [5,45;5,85) | 5 |
5,65 |
[5,85;6,25) |
9 |
6,05 |
[6,25;6,65) |
15 |
6,45 |
[6,65;7,05) |
19 |
6,85 |
[7,05;7,45) |
16 |
7,25 |
[7,45;7,85) |
8 |
7,65 |
[7,85;8,25) |
2 |
8,05 |
Cộng |
74 |
|
Áp dụng công thức ta tìm được số trung bình :
x = 5 , 65 . 5 + 6 , 05 . 9 + 6 , 45 . 15 + 6 , 85 . 19 + 7 , 25 . 16 + 7 , 65 . 8 + 8 , 05 . 2 74 ≈ 6 , 8
Đáp án là D.
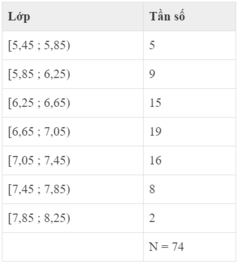
Chọn A.
Ta có bảng sau: