Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
CÁCH 1
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ”.
Ta xét các trường hợp:
TH1: Chọn được 1 nữ, 3 nam. Số cách chọn là: ![]()
TH2: Chọn được 2 nữ, 2 nam. Số cách chọn là: ![]() .
.
TH3: Chọn được 3 nữ, 1 nam. Số cách chọn là: ![]() .
.
Suy ra ![]()
Vậy xác suất cần tìm là: ![]()
CÁCH 2
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ” thì A ¯ là biến cố: “cả 4 học sinh được chọn chỉ có nam hoặc nữ”.
Ta có ![]()
Do đó xác suất xảy ra của biến cố
A
¯
là: 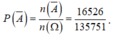
Suy ra ![]()

Chọn C
Gọi A: “4 học sinh được chọn có cả nam và nữ.”
=> A ¯ : “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ.”
Số cách để lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác: Ω = C 44 4
Số cách chọn 4 học sinh toàn là nam: C 25 4
Số cách chọn 4 học sinh toàn là nữ: C 19 4
Xác suất để 4 học sinh được chọn có cả nam và nữ:
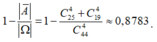

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 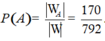
Chọn C.

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có ![]() cách.
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 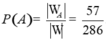
Chọn D.

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 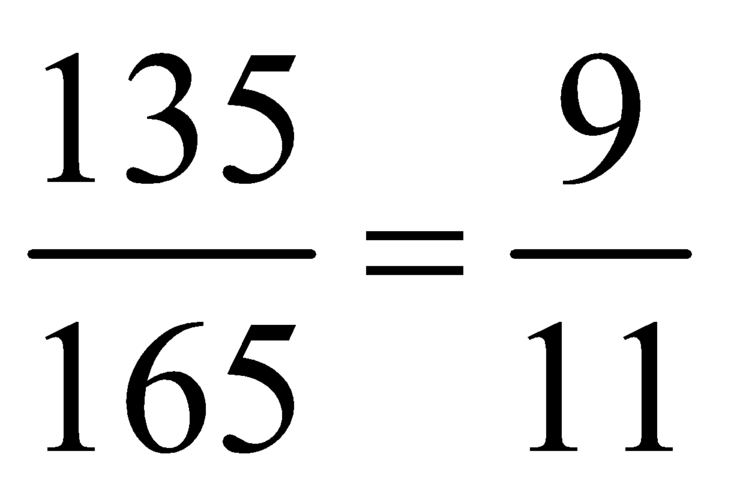 .
.



gọi số học sinh nữa là \(x\) \(\left(1\le x\le29;x\in Z\right)\)
\(\Rightarrow\) số học sinh nam là \(30-x\)
ta có : số cách để chọn 3 học sinh từ 30 học sinh là : \(C^3_{30}=4060\)
số cách để chọn 2 học sinh nam từ \(30-x\) học sinh nam là : \(C^2_{30-x}\)
số cách để chọn 1 học sinh nữ từ \(x\) học sinh nữ là : \(x\)
\(\Rightarrow\) sác xuất chọn được 2 nam và 1 nữ là : \(P=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{x.C^2_{30-x}}{4060}=\dfrac{12}{29}\)
\(\Leftrightarrow\dfrac{\dfrac{x\left(30-x\right)!}{2!\left(30-x-2\right)!}}{4060}=\dfrac{12}{29}\) \(\Leftrightarrow\dfrac{\dfrac{x\left(30-x\right)!}{2!\left(28-x!\right)}}{4060}=\dfrac{12}{29}\)
\(\Leftrightarrow\dfrac{x\left(29-x\right)\left(30-x\right)}{8120}=\dfrac{12}{29}\) \(\Leftrightarrow x^3-59x^2+870x-3360=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\simeq38,8\left(L\right)\\x\simeq6,2\left(L\right)\\x=14\left(N\right)\end{matrix}\right.\)
vậy có 14 học sinh nữ