Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Lời giải. Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * )
Suy ra số học sinh nữ trong nhóm B là
25 - 9 - x - y = 16 - x - y
Khi đó, nhóm A có: 9 nam, x nữ và nhóm B có
y nam, 16 - x - y nữ
Xác suất để chọn được hai học sinh nam là
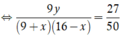
![]()
![]()
![]()
Mặt khác x + y < 16
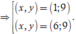
Vậy xác suất để chọn đươc hai học sinh nữ là
C 1 1 . C 6 1 C 10 1 . C 15 1 = 0 , 04

Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
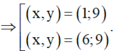
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.

Chọn B
Số cách chọn 2 học sinh trong 10 học sinh là C 10 2 .
Nên số phần tử của không gian mẫu là ![]() .
.
Gọi A : “ Biến cố chọn được hai học sinh đều là học sinh nữ”.
Số cách chọn 2 học sinh nữ trong 3 học sinh nữ là C 3 2 .
Khi đó số phần tử của biến cố A là n(A) = C 3 2 = 3.
Vậy xác suất để chọn được hai học sinh đều là nữ là 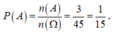

Chọn B
Ta có: ![]()
Gọi A là biến cố: “Chọn được một học sinh nữ”.
![]()
Xác suất để chọn được một học sinh nữ là: 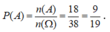

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 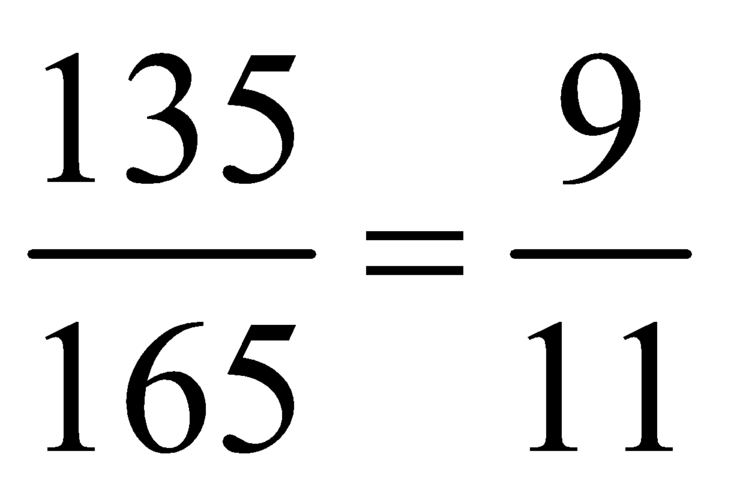 .
.

Lời giải:
a. Xác suất chọn hsg là:
$\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}=\frac{17}{50}$
b.
Chọn ngẫu nhiên 3 hs, có $C^3_{100}$ cách chọn
Số hsg là: $(\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}).100=34$ (hs)
Chọn ngẫu nhiên được 2 hsg có $C^2_{34}C^1_{100-34}=C^2_{34}.C^1_{66}$ cách chọn
Xác suất cần tìm: $p=\frac{C^2_{34}.C^1_{66}}{C^3_{100}}=\frac{561}{2450}$