Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 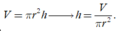
Gọi t là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá tiền của một đơn vị diện tích vật liệu để làm mặt đáy là 3t
Diện tích mặt xung quanh ![]() giá tiền mặt xung quanh là
giá tiền mặt xung quanh là ![]()
Diện tích hai mặt đáy ![]() giá tiền hai mặt đáy là
giá tiền hai mặt đáy là ![]()
Tổng tiền hoàn thành sản phẩm:
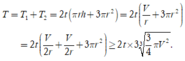
Dấu "=" xảy ra 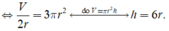
Chọn C.

Đáp án A.
Gọi r, h lần lượt là bán kính đáy, chiều cao của khối trụ.
Vì 2 x khối trụ nội tiếp khối cầu suy ra R 2 = r 2 + h 2 ⇔ r 2 + h 2 = 27 .
Thể tích của khối trụ là V = πr 2 h = π . h 27 - h 2 → f h = 27 h - h 3 .
Khảo sát hàm số f h → GTLN của f(h) là 54 khi h = 3.
Suy ra thể tích lớn nhất của khối trụ là V = 54 π cm 3 .
Số hoạt chất đặc biệt cần dùng để làm kem dưỡng da là 0 , 3 % . 54 π = 0 , 509 cm 3 .
Vậy số hộp kem tối đa mà công ty sản xuất được là 1 . 100 3 0 , 509 ≈ 1964875 hộp.

Ta có C ' x = 2 x 2 - 24 x + 70 x - 6 2
C ' x = 0 ⇔ x = 5 x = 7 So điều kiện x > 6, chọn x = 7
Vậy để tổng chi phí lớn nhất thì công ty cần cải tiến 7 đơn vị sản phẩm
Đáp án D

Đáp án A
Gọi R và h lần lượt là bán kính và chiều cao của 1 thùng sơn
Suy ra dung tích 1 thùng sơn: V = πR 2 h = 0 , 005 m 3
Gọi n là số thùng sơn tối đa sản xuất được
Tổng chi phí đó bỏ ra là: T = n × 100 . 000 × S x q + 120 . 000 × S d
= n × 100 . 000 × 2 πRh + 120 . 000 × 2 πR 2 ≤ 10 9 ⇔ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2
Mà 10 R h + 12 R 2 = 5 R h + 5 R h + 12 R 2 ≥ 3 300 R 4 h 2 3 = 3 300 V 2 π 2 3
⇒ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2 ≤ 5 × 10 4 π 3 × 300 V 2 π 2 3 ≈ 58135 , 9 ⇒ n = 58135 .

Mỗi thùng có bán kính đáy r chiều cao h(đơn vị mét) thể tích là ![]()
Chi phí làm mỗi thùng bằng ![]() (triệu đồng). Trước tiên ta cần tìm chi phí nhỏ nhất sản xuất mỗi thùng. Rút
(triệu đồng). Trước tiên ta cần tìm chi phí nhỏ nhất sản xuất mỗi thùng. Rút  thay vào
thay vào
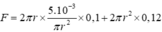
![]()
![]()
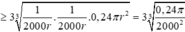
Số thùng tối đa công ty sản xuất được bằng  thùng.
thùng.
Chọn đáp án D.

Gọi bán kính hình trụ là x > 0.
Khi đó ta có diện tích của hai đáy thùng là S 1 = 2 πx 2 Diện tích xung quanh của thùng là S 2 = 2 πxh = 2 πx V πx 2 = 2 V x
trong đó h là chiều cao của thùng và từ V = πx 2 . h ⇒ h = V πx 2
Vậy diện tích toàn phần của thùng là S = S 1 + S 2 = 2 πx 2 + 2 V x
Để tiết kiệm vật liệu nhất thì S phải bé nhất. Áp dụng bất đẳng thức AM-GM ta có
S = 2 πx 2 + V 2 x + V 2 x ≥ 2 . 3 πV 2 4 3
Do đó S bé nhất khi và chỉ khi πx 2 = V 2 x ⇔ x = V 2 π 3
Đáp án A


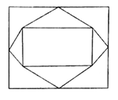
Đáp án B
Thể tích của mỗi thỏi son hình trụ là:
V = π r 2 h = 20 , 25 π ⇔ r 2 h = 20 , 25 ⇔ h = 20 , 25 r 2
Ta có:
T = 60000 r 2 + 20000 r h = 60000 r 2 + 20000 r . 20 , 25 r 2 = 60000 r 2 + 405000 r
60000 r 2 + 202500 r + 202500 r ≥ 3 60000 r 2 . 202500 r . 202500 r 3 = 405000
Dấu “=” xảy ra khi:
60000 r 2 = 202500 r ⇔ r = 3 2 ⇒ h = 9 ⇒ r + h = 10 , 5 c m