K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
11 tháng 2 2020
Gọi Vận tốc dự định để ca nô đi hết quãng đường AB là: x ( x > 0 ) ( giờ )
Thời gian là: y ( y > 0 ) ( km/h)
Quãng đường AB là: xy ( km)
Vì khi ca nô tăng 2 km/h thì đến nơi sớm 2 giờ
\(\Rightarrow\left(x+2\right).\left(y-2\right)=xy\)
\(\Leftrightarrow-2x+2y=4\)
\(\Leftrightarrow-x+y=2\left(1\right)\)
Vì khi ca nô giảm 2km/h thì đền nơi muộn 3 giờ
\(\Rightarrow\left(x-2\right).\left(y+3\right)=xy\)
\(\Leftrightarrow3x-2y=6\left(2\right)\)
Từ ( 1 ) và ( 2 ) ta có hệ phương trình:
\(\hept{\begin{cases}-x+y=2\\3x-2y=6\end{cases}\Leftrightarrow\hept{\begin{cases}x=10\\y=12\end{cases}}}\)
\(\Rightarrow\)Quãng đường AB là: 120 km
HM
5 tháng 7 2017
- Đề đầy đủ rồi nhé các bạn. KO CÓ cộng thêm căn xy bên phải đâu tại tớ nhìn bị thiếu á -.-
1 tháng 11 2023
1:
1: \(2\sqrt{12}+3\sqrt{18}-3\sqrt{75}-\sqrt{50}\)
\(=4\sqrt{3}-15\sqrt{3}+9\sqrt{2}-5\sqrt{2}\)
\(=-11\sqrt{3}+4\sqrt{2}\)
2: \(\sqrt{16-6\sqrt{7}}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{7}\right)^2}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\left|3-\sqrt{7}\right|+\left|3+\sqrt{7}\right|\)
\(=3-\sqrt{7}+3+\sqrt{7}=6\)
3:
\(\dfrac{6}{\sqrt{7}-1}+\dfrac{4}{\sqrt{7}-3}+\dfrac{7}{\sqrt{7}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-\dfrac{4}{3-\sqrt{7}}+\sqrt{7}\)
\(=\sqrt{7}+1+\sqrt{7}-\dfrac{4\left(3+\sqrt{7}\right)}{2}\)
\(=2\sqrt{7}+1-2\left(3+\sqrt{7}\right)\)
=1-6
=-5
2:
a: ĐKXĐ: x>=5
\(5\sqrt{x-5}+\sqrt{4x-20}-\sqrt{9x-45}=12\)
=>\(5\sqrt{x-5}+2\sqrt{x-5}-3\sqrt{x-5}=12\)
=>\(4\sqrt{x-5}=12\)
=>\(\sqrt{x-5}=3\)
=>x-5=9
=>x=14(nhận)
2:
ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2-20x+25}=1\)
=>\(4x^2-20x+25=1\)
=>(2x-5)2=1
=>\(\left[{}\begin{matrix}2x-5=1\\2x-5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
23 tháng 7 2021
b) Thay x=0 và y=0 vào (d), ta được:
\(2m\cdot0+3-m-0=0\)
\(\Leftrightarrow3-m=0\)
hay m=3
c) Thay x=2 và y=0 vào (d), ta được:
\(2m\cdot2+3-m-2=0\)
\(\Leftrightarrow3m=-1\)
hay \(m=-\dfrac{1}{3}\)
9 tháng 9 2021
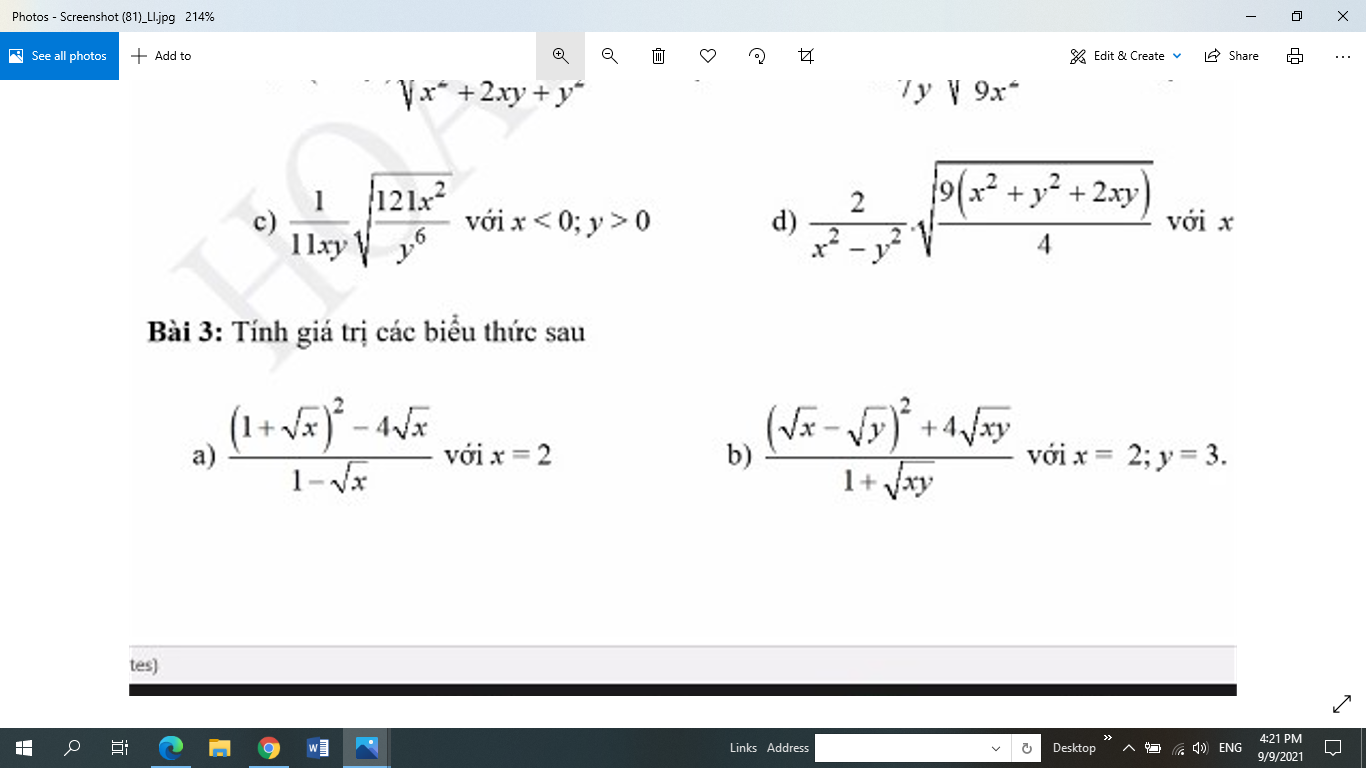
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)
N
25 tháng 8 2019
a.\(DK:\frac{2}{3}\le x< 4\)
b.\(DK:x>\frac{1}{2},x\ne\frac{5}{2}\)
c.\(DK:x\le-3\)
25 tháng 8 2019
Bạn MaiLink ơi, bạn có thể ghi rõ ra các bước làm được không? mình không hiểu lắm. cảm ơn bạn
2 tháng 9 2021
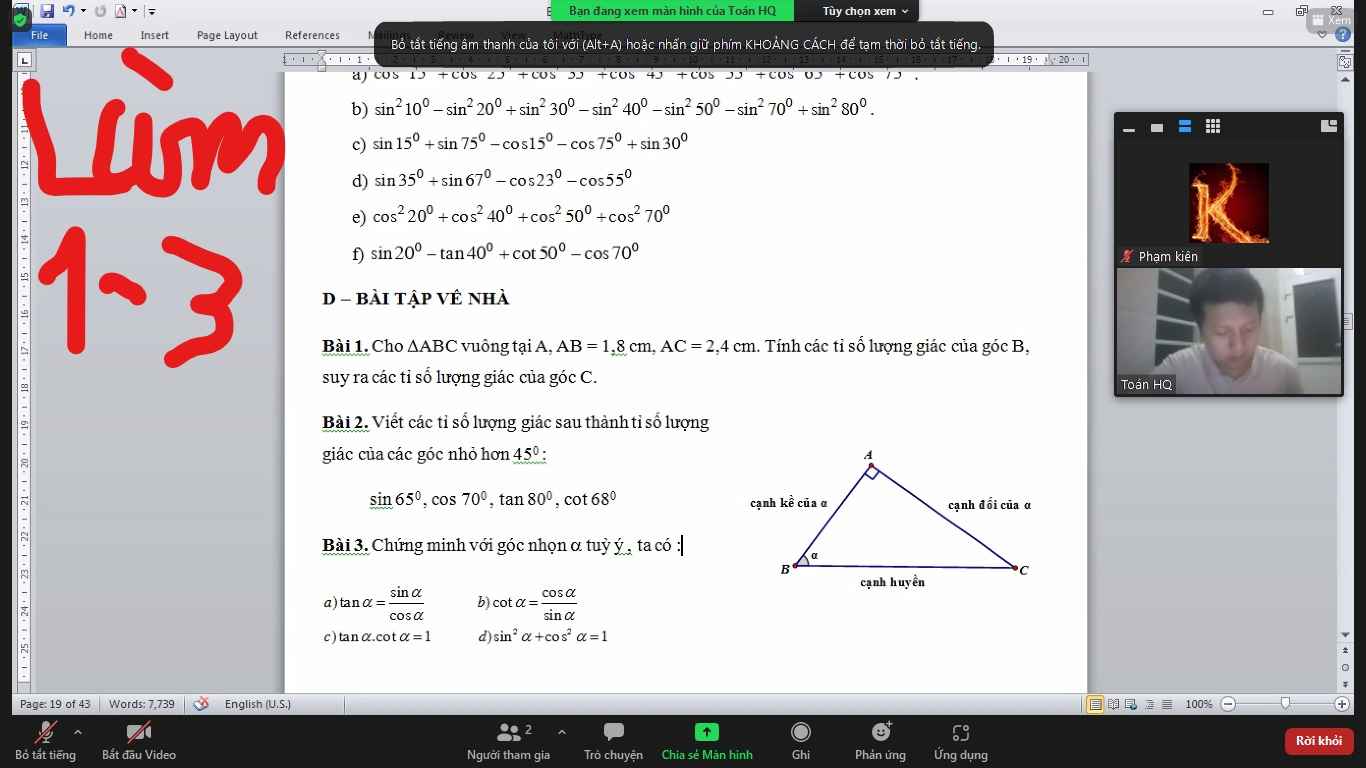
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)
NL
0
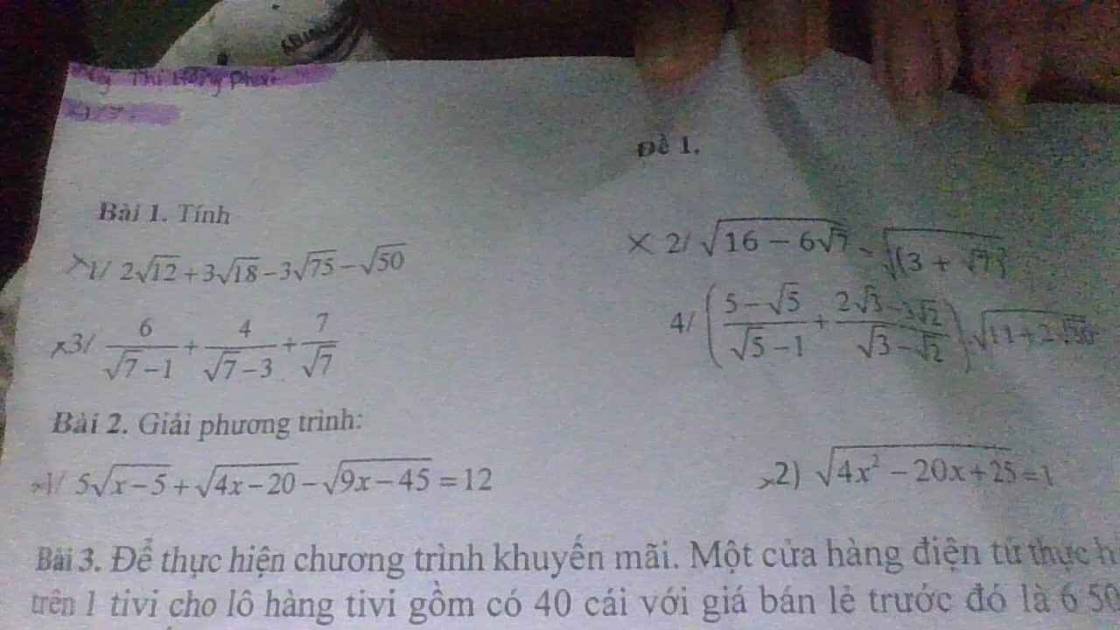
\(ĐKXĐ:a>0,a\ne\pm1\)
Có : \(P=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}+\dfrac{\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{3}\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}+\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\dfrac{\sqrt{a}+1}{3}\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{3}\)
\(=\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\cdot\dfrac{3}{\sqrt{a}+1}=\dfrac{3}{\sqrt{a}-1}\)
Vậy \(P=\dfrac{3}{\sqrt{x}-1}\) với \(x>0,x\ne\pm1\)