K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HELP ME PLEASE!!!!!mai tớ thi rr các cậu ơi
1 tháng 11 2023
1:
1: \(2\sqrt{12}+3\sqrt{18}-3\sqrt{75}-\sqrt{50}\)
\(=4\sqrt{3}-15\sqrt{3}+9\sqrt{2}-5\sqrt{2}\)
\(=-11\sqrt{3}+4\sqrt{2}\)
2: \(\sqrt{16-6\sqrt{7}}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{7}\right)^2}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\left|3-\sqrt{7}\right|+\left|3+\sqrt{7}\right|\)
\(=3-\sqrt{7}+3+\sqrt{7}=6\)
3:
\(\dfrac{6}{\sqrt{7}-1}+\dfrac{4}{\sqrt{7}-3}+\dfrac{7}{\sqrt{7}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-\dfrac{4}{3-\sqrt{7}}+\sqrt{7}\)
\(=\sqrt{7}+1+\sqrt{7}-\dfrac{4\left(3+\sqrt{7}\right)}{2}\)
\(=2\sqrt{7}+1-2\left(3+\sqrt{7}\right)\)
=1-6
=-5
2:
a: ĐKXĐ: x>=5
\(5\sqrt{x-5}+\sqrt{4x-20}-\sqrt{9x-45}=12\)
=>\(5\sqrt{x-5}+2\sqrt{x-5}-3\sqrt{x-5}=12\)
=>\(4\sqrt{x-5}=12\)
=>\(\sqrt{x-5}=3\)
=>x-5=9
=>x=14(nhận)
2:
ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2-20x+25}=1\)
=>\(4x^2-20x+25=1\)
=>(2x-5)2=1
=>\(\left[{}\begin{matrix}2x-5=1\\2x-5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
9 tháng 7 2023
b: ΔOBA vuông tại B có BI là đường cao
nên OI*IA=BI^2
=>OI*OA=1/4BC^2
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=AD/AB
=>AE*AD=AB^2=AB*AC
TL
0
17 tháng 11 2021
Bài 15:
\(a,ĐK:y>0;y\ne1\\ b,Q=\left[\dfrac{\sqrt{y}\left(\sqrt{y}-1\right)}{\sqrt{y}-1}-\dfrac{\sqrt{y}+1}{\sqrt{y}\left(\sqrt{y}+1\right)}\right]\cdot\dfrac{y}{\sqrt{y}+1}\\ Q=\left(\sqrt{y}-\dfrac{1}{\sqrt{y}}\right)\cdot\dfrac{y}{\sqrt{y}+1}=\dfrac{y-1}{\sqrt{y}}\cdot\dfrac{y}{\sqrt{y}+1}\\ Q=\sqrt{y}\left(\sqrt{y}-1\right)\\ c,Q=y-\sqrt{y}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{y}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\\ Q_{min}=-\dfrac{1}{4}\Leftrightarrow\sqrt{y}=\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{4}\left(tm\right)\)
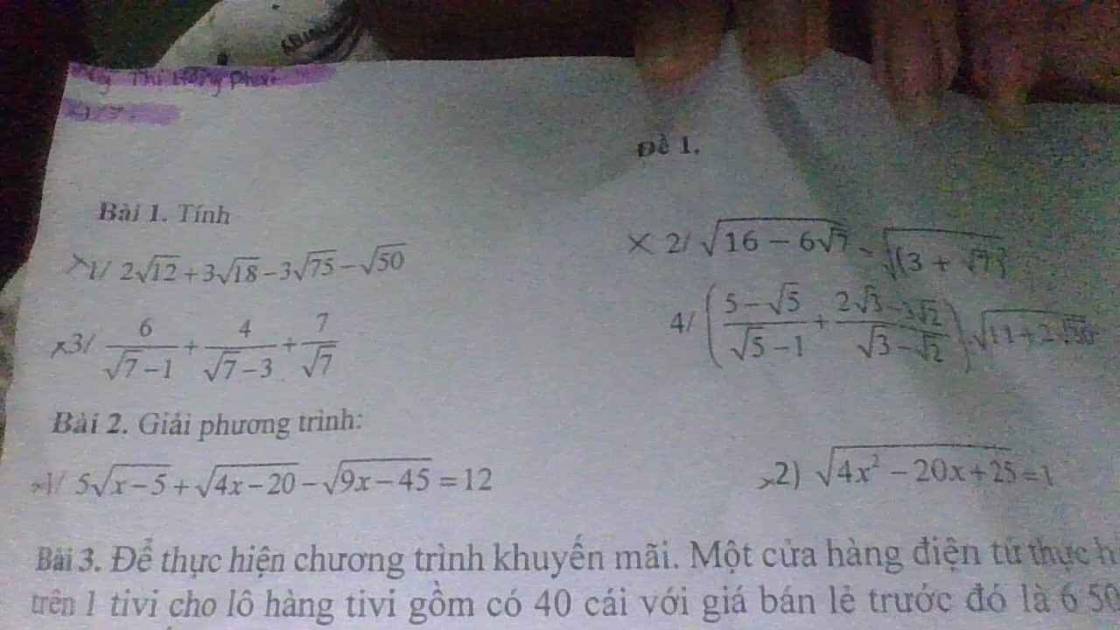
b) Thay x=0 và y=0 vào (d), ta được:
\(2m\cdot0+3-m-0=0\)
\(\Leftrightarrow3-m=0\)
hay m=3
c) Thay x=2 và y=0 vào (d), ta được:
\(2m\cdot2+3-m-2=0\)
\(\Leftrightarrow3m=-1\)
hay \(m=-\dfrac{1}{3}\)