Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mọi người ơi làm giúp mình nha (làm 1 câu cũng được, 2 câu cũng được, mình tick tất nha)
a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
b: Xét ΔEAD có
EB là đường cao
EB là đường trung tuyếm
Do đó: ΔEAD cân tại E
b:
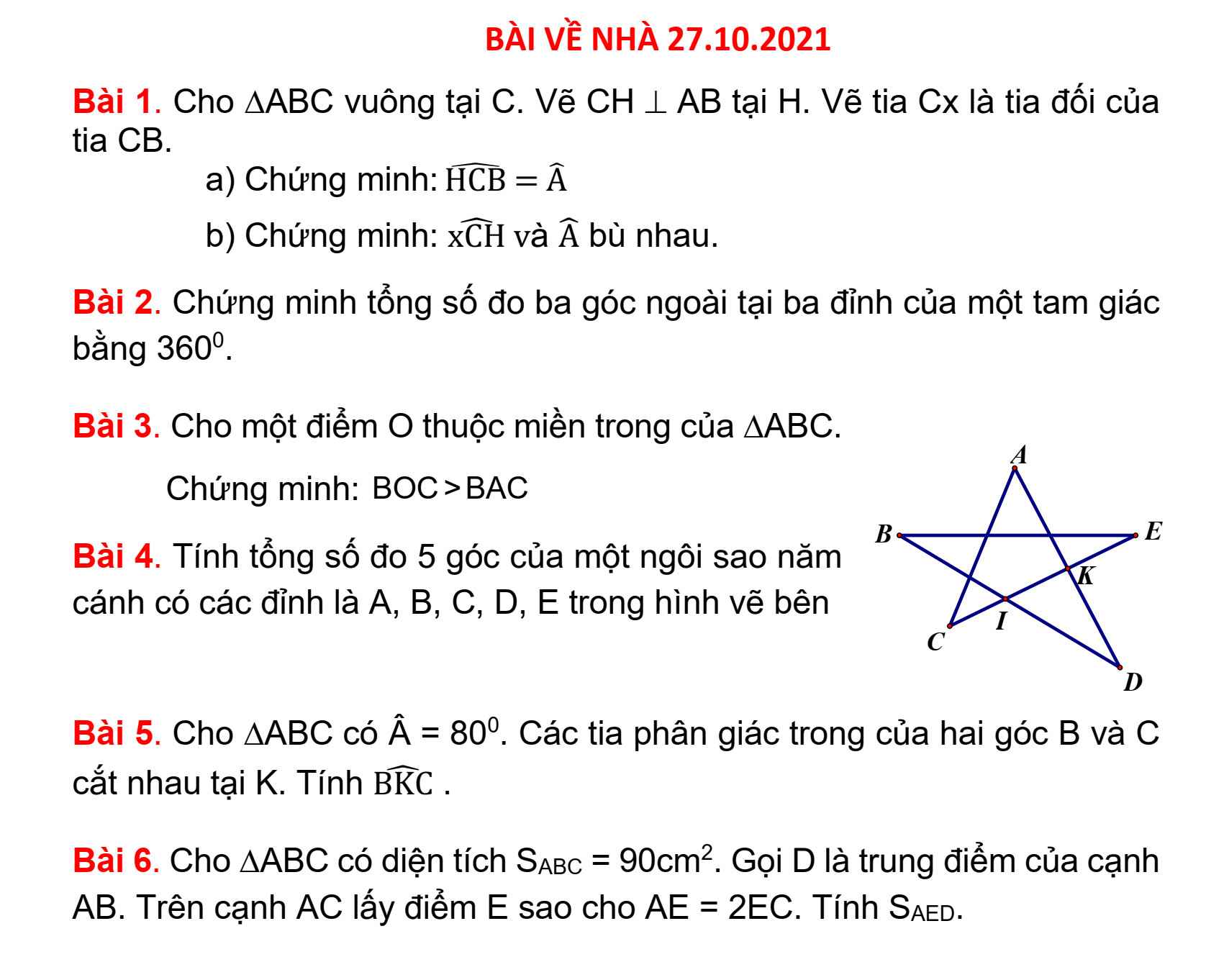
Bài 5:
\(\widehat{BKC}=180^0-\left(\widehat{KBC}+\widehat{KCB}\right)\)
\(=180^0-\dfrac{180^0-80^0}{2}\)
\(=180^0-50^0=130^0\)
Bài 7:
a) Ta có: x:2=y:5
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=3\\\dfrac{y}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=15\end{matrix}\right.\)
c) Ta có: x:2=y:7
nên \(\dfrac{x}{2}=\dfrac{y}{7}\)
mà x+y=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{x+y}{2+7}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=2\\\dfrac{y}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=14\end{matrix}\right.\)
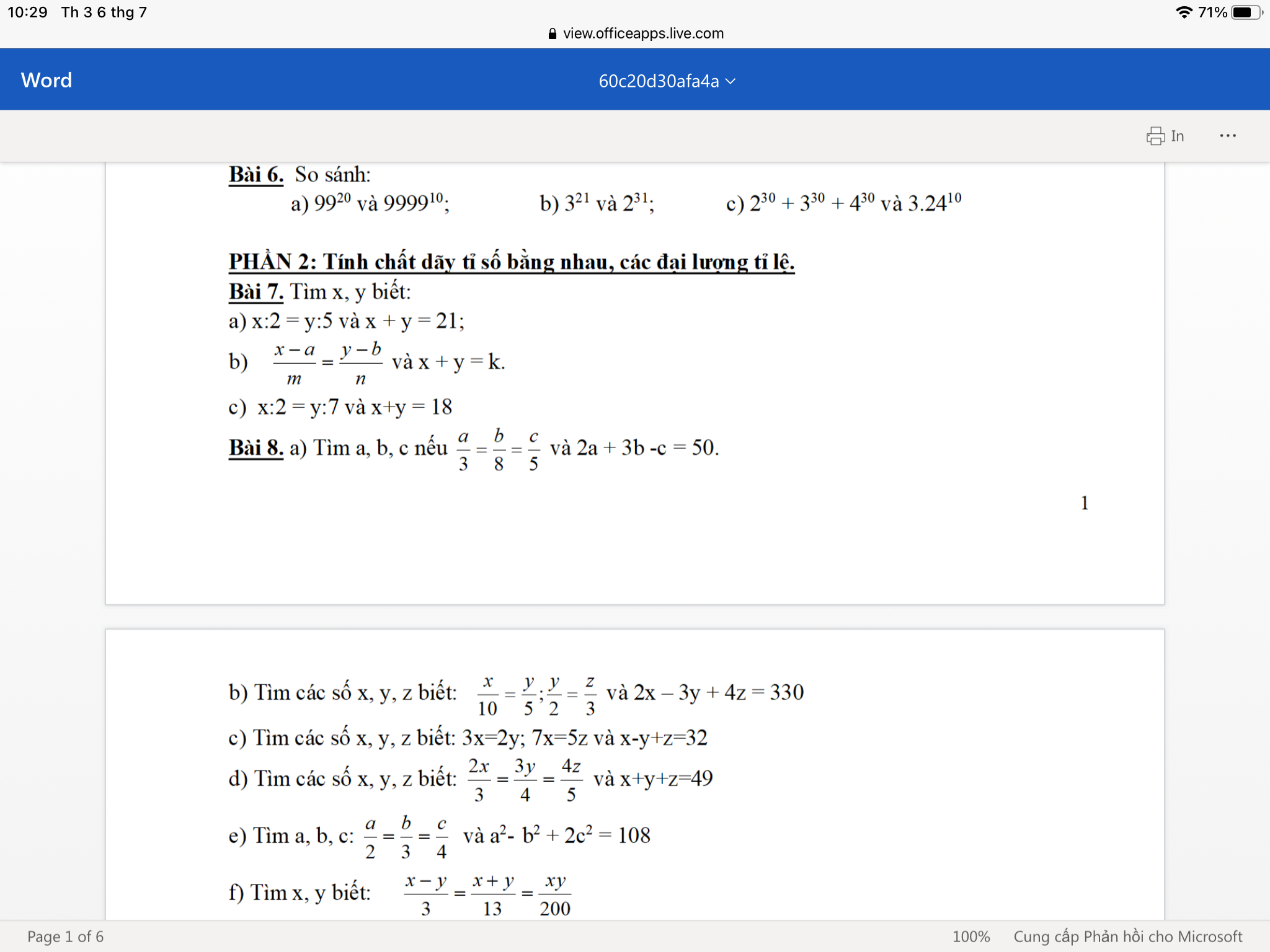
Bài 8:
a) Ta có: \(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\)
nên \(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}\)
mà 2a+3b-c=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}=\dfrac{2a+3b-c}{6+24-5}=\dfrac{50}{25}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{8}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=16\\c=10\end{matrix}\right.\)
Bài 8:
b) Ta có: \(\dfrac{x}{10}=\dfrac{y}{5}\)
nên \(\dfrac{x}{20}=\dfrac{y}{10}\)(1)
Ta có: \(\dfrac{y}{2}=\dfrac{z}{3}\)
nên \(\dfrac{y}{10}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
\(\Leftrightarrow\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}\)
mà 2x-3y+4z=330
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}=\dfrac{2x-3y+4z}{40-30+60}=\dfrac{330}{70}=\dfrac{33}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=\dfrac{33}{7}\\\dfrac{y}{10}=\dfrac{33}{7}\\\dfrac{z}{15}=\dfrac{33}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{660}{7}\\y=\dfrac{330}{7}\\z=\dfrac{495}{7}\end{matrix}\right.\)
c) Ta có: 3x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
hay \(\dfrac{x}{10}=\dfrac{y}{15}\)(1)
Ta có: 7x=5z
nên \(\dfrac{x}{5}=\dfrac{z}{7}\)
hay \(\dfrac{x}{10}=\dfrac{z}{14}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x-y+z}{10-15+14}=\dfrac{32}{9}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{10}=\dfrac{32}{9}\\\dfrac{y}{15}=\dfrac{32}{9}\\\dfrac{z}{14}=\dfrac{32}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{320}{9}\\y=\dfrac{480}{9}=\dfrac{160}{3}\\z=\dfrac{448}{9}\end{matrix}\right.\)
ko sao à.mik kiểm tra lại thì thấy bạn đúng à.cảm ơn bạn nhiều 
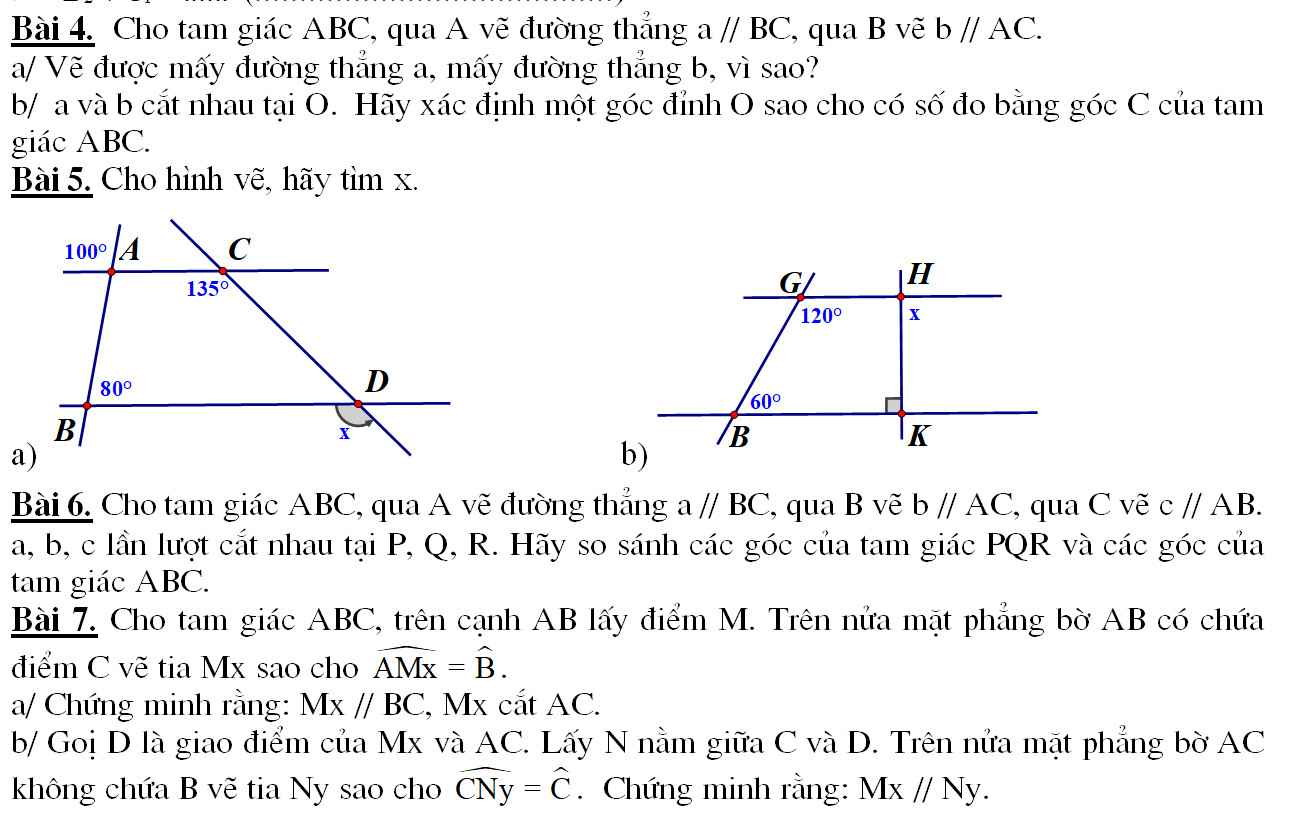
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
Đặt cái bt ở trên là A thì 3^4.A=81 A=3^4+3^8+3^12+3^16 mà A=1+3^4+3^8+3^12>>>80A=3^16-1>>A=(3^16-1)/80.
Tương tự thì B(bt ở mẫu)=(3^16-1)/8.
>>A/b=(1/80)/(1/8)=1/10
Vậy GTBT là 1/10
mình kho ghi lại đề nha
giải
đề ( ghi lại )
= \(\frac{1+81+6561+312}{1+9+81+729+6561+59049+312+314}\)
=\(\frac{6643+312}{91+719+6561+59049+312+314}\)
=\(\frac{6643+312}{66430+312+1314}\)
\(a,\frac{5}{6}-2\sqrt{\frac{4}{9}}+\sqrt{\left(-2\right)^2}\)
\(=\frac{5}{6}-2.\frac{2}{3}+2\)
\(=\frac{5}{6}-\frac{4}{6}+\frac{12}{6}\)
\(=\frac{5-4+12}{6}=\frac{13}{6}\)
\(b,\left(-3\right)^2.\left(\frac{1}{3}\right)^3:\left[\left(-\frac{2}{3}\right)^3-1\frac{1}{3}\right]-\left(-200\right)^0\)
\(=9.\frac{1}{27}:\left(-\frac{8}{27}-\frac{5}{3}\right)-1\)
\(=\frac{1}{3}:\left(-\frac{8}{27}-\frac{45}{27}\right)-1\)
\(=\frac{1}{3}:\left(-\frac{53}{27}\right)-1\)
\(=\frac{1}{3}.\left(-\frac{27}{53}\right)-1\)
\(=-\frac{9}{53}-1=-\frac{9}{53}-\frac{53}{53}\)
\(=-\frac{62}{53}\)
\(c,\left(-0,5-\frac{3}{5}\right):\left(-3\right)+\frac{1}{3}-\left(-\frac{1}{6}\right):2\)
\(=\left(-\frac{1}{2}-\frac{3}{5}\right).\frac{1}{3}+\frac{1}{3}-\left(-\frac{1}{6}\right).\left(-\frac{1}{2}\right)\)
\(=\left(-\frac{5}{10}-\frac{6}{10}\right).\frac{1}{3}+\frac{1}{3}-\frac{1}{12}\)
\(=-\frac{11}{10}.\frac{1}{3}+\frac{1}{3}-\frac{1}{12}\)
\(=\frac{1}{3}\left(-\frac{11}{10}-\frac{1}{12}\right)\)
\(=\frac{1}{3}\left(-\frac{66}{60}-\frac{5}{60}\right)\)
\(=\frac{1}{3}.\left(-\frac{71}{60}\right)\)
\(=-\frac{71}{180}\)