
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
1.\(x\left(x+3\right)\)
\(=x^2+3x\)
2.\(3x\left(x+2\right)\)
\(=3x^2+6x\)
3,\(x^2\left(3x-1\right)\)
\(=3x^3-x^2\)
4.\(-5x^3\left(3x^2-7\right)\)
\(=-15x^5+35x^3\)
5.\(3x\left(5x^2-2x-1\right)\)
\(=15x^3-6x^2-3x\)
6.\(-x^2\left(5x^3-x-\dfrac{1}{2}\right)\)
\(=-5x^5+x^3+\dfrac{x^2}{2}\)
7.\(\left(x^2+2x-3\right).\left(-x\right)\)
\(=-x^3-2x^2+3x\)
8.\(4x^3\left(-2x^2+4x^4-3\right)\)
\(=-8x^5+16x^7-12x^3\)
9.\(-5x^2\left(3x^2-2x+1\right)\)
\(=-15x^4+10x^3-5x^2\)
10.\(-4x^5\left(x^3-4x^2+7x-3\right)\)
\(=-4x^8+16x^7-28x^6+12x^5\)
11.\(\left(x+2\right)\left(x+3\right)\)
\(=x^2+3x+2x+6\)
12.\(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
13.\(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
14.\(\left(x-3\right)\left(x^2-2x-1\right)\)
\(x^3-2x^2-x-3x^2+6x+3\)
15.\(\left(2x-1\right)\left(x^2-5x+3\right)\)
\(=2x^3-10x^2+6x-x^2+5x-3\)
16.\(\left(x-5\right)\left(-x^2+x-1\right)\)
\(=-x^3+x^2-x+5x^2-5x+5\)
17,\(\left(\dfrac{1}{2}x+3\right)\left(2x^2-4x-6\right)\)
\(=x^3-2x^2-3x+6x^2-12x-18\)
P/s:mình làm hơi tắt tại bài dài quá:))

\(\frac{4}{3}-\left(x-\frac{1}{5}\right)=\left|\frac{-3}{10}+\frac{1}{2}\right|-\frac{1}{6}\)
\(\frac{4}{3}-\left(x-\frac{1}{5}\right)=\frac{1}{5}-\frac{1}{6}\)
\(\frac{4}{3}-\left(x-\frac{1}{5}\right)=\frac{1}{30}\)
\(x-\frac{1}{5}=\frac{4}{3}-\frac{1}{30}\)
\(x-\frac{1}{5}=\frac{13}{10}\)
\(x=\frac{13}{10}+\frac{1}{5}\)
\(x=\frac{3}{2}\)

`a,`
`P(x)=x^2-5+x^4-4x^3-x^6`
`P(x)= -x^6+x^4-4x^3+x^2-5`
`Q(x)=2x^5-x^4+x^2-x^3+x-1`
`Q(x)=2x^5-x^4-x^3+x^2+x-1`
`b,`
`P(x)+Q(x)=(-x^6+x^4-4x^3+x^2-5)+(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1`
`= -x^6+2x^5+(x^4-x^4)+(-4x^3-x^3)+(x^2+x^2)+x+(-5-1)`
`= -x^6+2x^5-5x^3+2x^2+x-6`
`c,`
`P(x)-Q(x)=(-x^6+x^4-4x^3+x^2-5)-(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2-x+1`
`= -x^6-2x^5+(x^4+x^4)+(-4x^3+x^3)+(x^2-x^2)+x+(-5+1)`
`= -x^6-2x^5+2x^4-3x^3+x-4`
Ote.
Phần trừ đa thức một biến, bạn phải chú ý trước có dấu trừ, bạn ngoặc vào nhé! Còn trước dấu ngoặc có dấu trừ, đổi dấu. Khi gộp và rút gọn các đa thức cùng bậc, chú ý trước dấu ngoặc nên để dấu cộng, khi gộp vào phải đưa nguyên dấu của hạng tử, không được tự tiện đổi. Những cái này là phải nhớ nhé!

Bài 4:
a: Đặt \(A=\dfrac{1}{2}x^2\left(-2x^2y^2z\right)\cdot\dfrac{-1}{3}x^2y^3\)
\(=\left(\dfrac{1}{2}\cdot\left(-2\right)\cdot\dfrac{-1}{3}\right)\cdot\left(x^2\cdot x^2\cdot x^2\right)\cdot y^5z\)
\(=-\dfrac{1}{3}x^6y^5z\)
bậc là 6+5+1=12
Thay x=-1/2 và y=2 vào A, ta được:
\(A=-\dfrac{1}{3}\cdot\left(-\dfrac{1}{2}\right)^6\cdot2^5\cdot z=-\dfrac{1}{3}z\cdot\dfrac{1}{2}=-\dfrac{1}{6}z\)
b: Đặt \(B=\left(-x^2y\right)^3\cdot\dfrac{1}{2}x^2y^3\cdot\left(-2xy^2z\right)^2\)
\(=-x^6y^3\cdot\dfrac{1}{2}x^2y^3\cdot4x^2y^4z^2\)
\(=-2x^{10}y^{10}z^2\)
Bậc là 10+10+2=22
Thay x=-1/2 và y=2 vào B, ta được:
\(B=-2\cdot\left(-\dfrac{1}{2}\right)^{10}\cdot2^{10}\cdot z^2=-2z^2\)
c: Đặt \(C=\left(-6x^3yz\right)\cdot\left(\dfrac{2}{3}x^2y\right)^2\)
\(=-6x^3yz\cdot\dfrac{4}{9}x^4y^2\)
\(=-\dfrac{8}{3}x^7y^3z\)
bậc là 7+3+1=11
Thay x=-1/2 và y=2 vào C, ta được:
\(C=-\dfrac{8}{3}\cdot\left(-\dfrac{1}{2}\right)^7\cdot2^3\cdot z=\dfrac{1}{6}z\)

Bài 3:
1: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\)
Do đó: x=14; y=26

Bài 5:
Vì \(\frac{x}{10}=\frac{y}{15}=\frac{z}{12}\)\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{12}=\frac{x-y+z}{10-15+12}=-\frac{49}{7}=-7\)
\(\Rightarrow x=-7.10=-70;y=-7.15=-105;z=-7.12=-84\)
Vậy x = -70; y = -105; z = -84
Bài 6:
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)\(\Rightarrow\frac{x^2}{2^2}=\frac{y^2}{3^2}=\frac{z^2}{4^2}=\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}\)
\(\Rightarrow\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}=\frac{2.z^2}{2.16}=\frac{2z^2}{32}=\frac{x^2-y^2+2z^2}{4-9+32}=\frac{108}{27}=4\)
\(\Rightarrow x^2=4.4=16\Rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)
\(y^2=9.4=36\Rightarrow\orbr{\begin{cases}y=6\\y=-6\end{cases}}\)
\(z^2=4.16=64\Rightarrow\orbr{\begin{cases}z=8\\z=-8\end{cases}}\)
Vậy x = 4; y = 6; z = 8 hoặc x = -4; y = -6; z = -8.
6, TA CÓ :
\(\frac{x^2}{4}\) =\(\frac{y^2}{9}\)=\(\frac{2z^2}{32}\)và x2 -y2 + 2z2 =108
ÁP DỤNG TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU :
TA CÓ :\(\frac{x^2}{4}\) - \(\frac{y^2}{9}\)+ \(\frac{2z^2}{32}\)=\(\frac{x^2-y^2+2z^2}{4-9+32}\)=\(\frac{108}{27}=4\)
=> \(x^2=4.4=16\)=> x = \(\sqrt{16}=4\)
\(y^2=9.4=36\Rightarrow y=\sqrt{36}=6\)
\(2z^2=32.4=128\Rightarrow z^2=\frac{128}{2}=64\Rightarrow z=\sqrt{64}=8\)

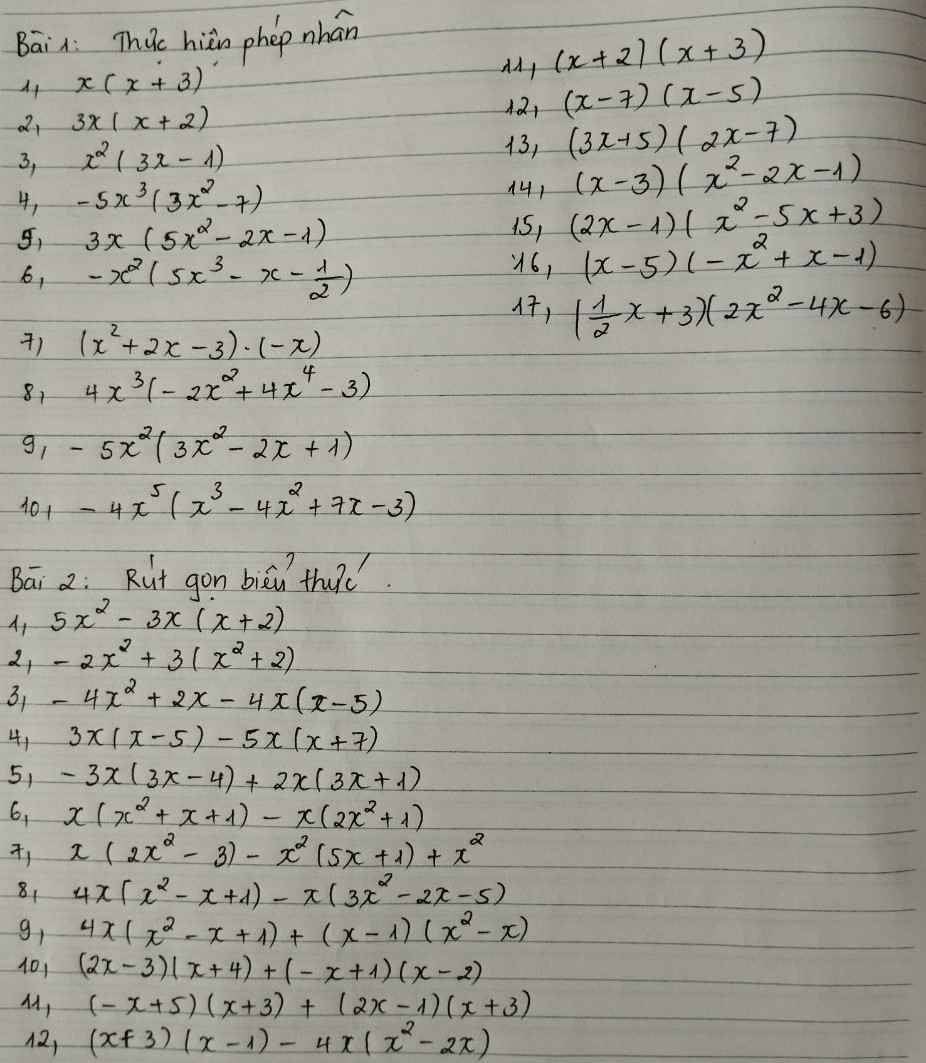
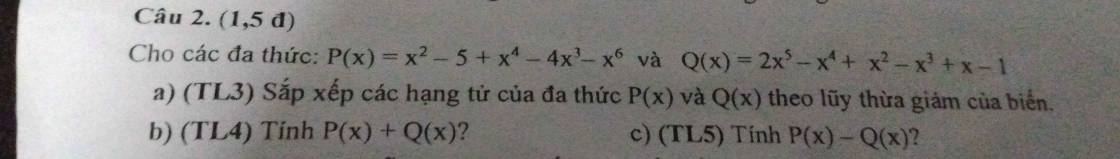 giải giúp mình nhé, cảm ơn mọi người và vote 5 điểm nha
giải giúp mình nhé, cảm ơn mọi người và vote 5 điểm nha

 Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!
Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!
Bài 5:
a, a \(\perp\) m; b \(\perp\) m ⇒ ⇒ a//b (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
b, \(\widehat{ABb}\) = \(\widehat{aAn}\) = 1300 (hai góc đồng vị)
\(\widehat{Fan}\) = 1800 - 1300 = 500