
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2 :
a) Góc ABC và Góc BCD là hai góc TRONG CÙNG PHÍA
b) Góc CMN và Góc CAD là hai góc ĐỒNG VỊ
c) Góc CMN và góc DNM là hai góc SO LE TRONG
d) Góc DAC và Góc ACB là hai góc SO LE TRONG
e) Góc CBA và Góc DAB là hai góc TRONG CÙNG PHÍA '
CỦA BẠN ĐÂY NHÉ :3
Chúc bạn học tốt !!!

\(\left[{}\begin{matrix}x-1,7=2,3\\x-1,7=-2,3\end{matrix}\right.\left[{}\begin{matrix}x=4\\x\neg-\dfrac{3}{5}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)

Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\) => \(\frac{x^2}{4}=\frac{y^2}{9}=\frac{2z^2}{32}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{4}=\frac{y^2}{9}=\frac{2z^2}{32}=\frac{x^2+y^2-2z^2}{4+9-32}=\frac{76}{-19}=-4\)
=> \(\hept{\begin{cases}\frac{x^2}{4}=-4\\\frac{y^2}{9}=-4\\\frac{2z^2}{32}=-4\end{cases}}\) => \(\hept{\begin{cases}x^2=-4.4=-16\\y^2=-4.9=-36\\z^2=\left(-4.32\right):2=-64\end{cases}}\) => ko có giá trị x,y,z thõa mãn
Ta có: \(-2x=5y\) => \(\frac{x}{5}=\frac{y}{-2}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5}=\frac{y}{-2}=\frac{x+y}{5-2}=\frac{30}{3}=10\)
=> \(\hept{\begin{cases}\frac{x}{5}=10\\\frac{y}{-2}=10\end{cases}}\) => \(\hept{\begin{cases}x=10.5=50\\y=10.\left(-2\right)=-20\end{cases}}\)
Vậy ..
\(\frac{x}{-3}=\frac{y}{-7}\Rightarrow\frac{2x}{-6}=\frac{4y}{-28}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{-6}=\frac{4y}{-28}=\frac{2x+4y}{(-6)+(-28)}=\frac{68}{-34}=-2\)
Vậy : \(\hept{\begin{cases}\frac{x}{-3}=-2\\\frac{y}{-7}=-2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=14\end{cases}}\)

\(P\left(0\right)=a\cdot0^3+b\cdot0^3+c\cdot0+d=2017\)
\(\Leftrightarrow d=2017\)
\(P\left(1\right)=a\cdot1^3+b\cdot1^2+c\cdot1+d=2\)
\(\Leftrightarrow a+b+a+d=2\)
\(P\left(-1\right)=a\cdot\left(-1\right)^3+b\cdot\left(-1\right)^2+c\cdot\left(-1\right)+d=6\)
\(\Leftrightarrow-a+b-c+d=6\)
\(P\left(2\right)=a\cdot2^3+b\cdot2^2+c\cdot2+d=-6033\)
\(\Leftrightarrow8a+4b+2c+d=-6033\)


Bài 7:
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: AB=AE
DB=DE(ΔABD=ΔAED)
=>AD là trung trực của BE
c: Xét ΔDBK và ΔDEC có
góc DBK=góc DEC
DB=DE
góc BDK=góc EDC
=>ΔDBK=ΔDEC
d: ΔDBK=ΔDEC
=>BK=EC
AK=AB+BK
AC=AE+EC
mà AB=AE; BK=EC
nên AK=AC
=>ΔAKC cân tai A
e: AK=AC
DK=DC
=>AD là trung trực của KC
=>AD vuông góc KC

Hướng dẫn thoai , bìa này tư duy đc :))
a) các cặp song song là : QE//PH;PQ//FH
b)
Góc EOQ = 90o - góc OQE = 90o- 55o = 35o
Góc OFH = 90o - góc EOQ = 90o - 35o = 55o
Góc PHF = 90o - góc OFH = 90o - 55o = 35o
 Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!
Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!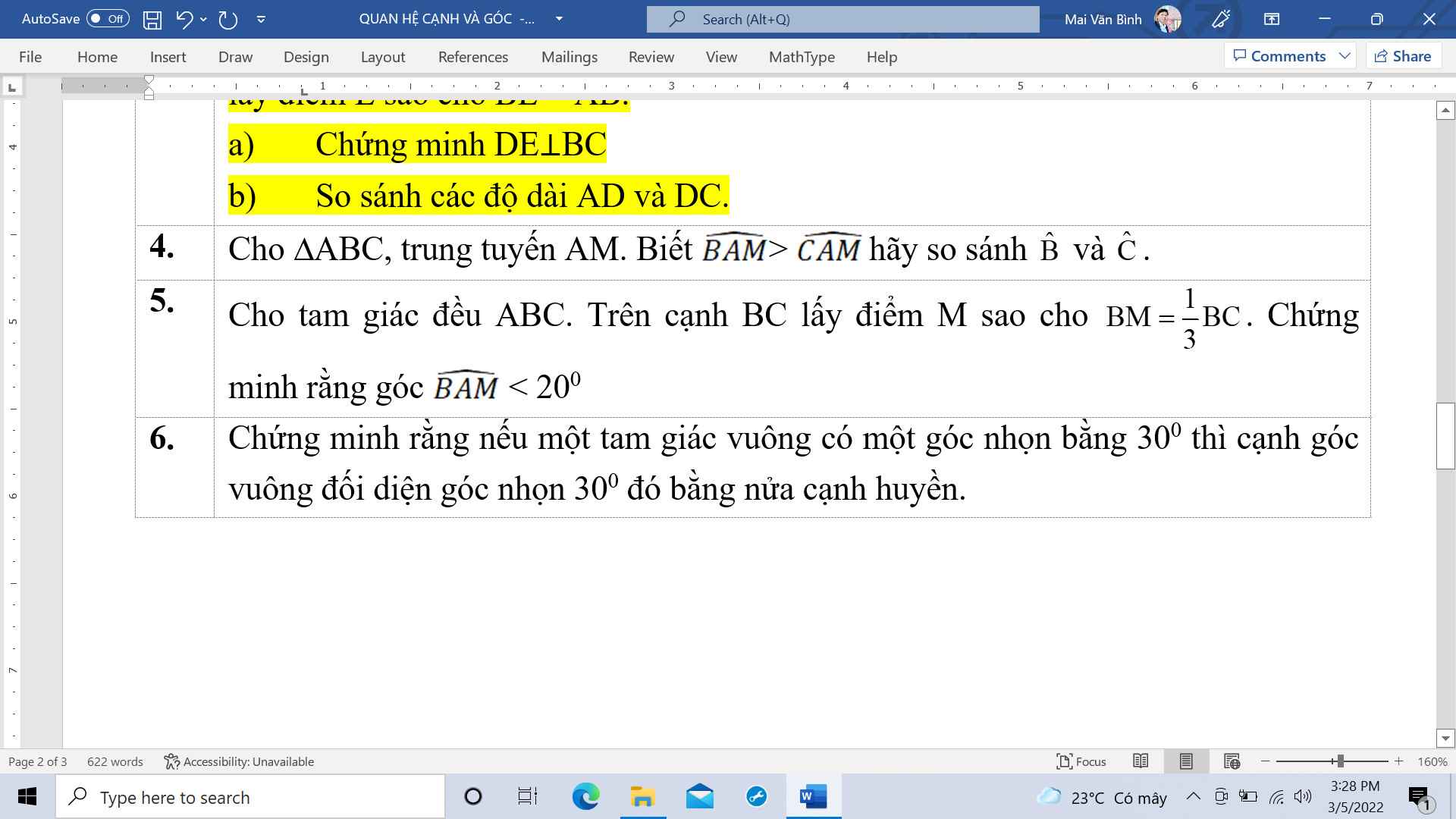



 các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II

Bài 5:
Vì \(\frac{x}{10}=\frac{y}{15}=\frac{z}{12}\)\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{12}=\frac{x-y+z}{10-15+12}=-\frac{49}{7}=-7\)
\(\Rightarrow x=-7.10=-70;y=-7.15=-105;z=-7.12=-84\)
Vậy x = -70; y = -105; z = -84
Bài 6:
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)\(\Rightarrow\frac{x^2}{2^2}=\frac{y^2}{3^2}=\frac{z^2}{4^2}=\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}\)
\(\Rightarrow\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}=\frac{2.z^2}{2.16}=\frac{2z^2}{32}=\frac{x^2-y^2+2z^2}{4-9+32}=\frac{108}{27}=4\)
\(\Rightarrow x^2=4.4=16\Rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)
\(y^2=9.4=36\Rightarrow\orbr{\begin{cases}y=6\\y=-6\end{cases}}\)
\(z^2=4.16=64\Rightarrow\orbr{\begin{cases}z=8\\z=-8\end{cases}}\)
Vậy x = 4; y = 6; z = 8 hoặc x = -4; y = -6; z = -8.
6, TA CÓ :
\(\frac{x^2}{4}\) =\(\frac{y^2}{9}\)=\(\frac{2z^2}{32}\)và x2 -y2 + 2z2 =108
ÁP DỤNG TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU :
TA CÓ :\(\frac{x^2}{4}\) - \(\frac{y^2}{9}\)+ \(\frac{2z^2}{32}\)=\(\frac{x^2-y^2+2z^2}{4-9+32}\)=\(\frac{108}{27}=4\)
=> \(x^2=4.4=16\)=> x = \(\sqrt{16}=4\)
\(y^2=9.4=36\Rightarrow y=\sqrt{36}=6\)
\(2z^2=32.4=128\Rightarrow z^2=\frac{128}{2}=64\Rightarrow z=\sqrt{64}=8\)