K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 10 2021
Bài 50:
1: \(\left(4-x\right)^2-16=0\)
\(\Leftrightarrow x\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=8\end{matrix}\right.\)
3: \(x^2-6x+9-16=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
1 tháng 3 2022
a: 3x-6=0
nên 3x=6
hay x=2
b: -2x+10=0
=>-2x=-10
hay x=5
c: -4x-12=0
=>-4x=12
hay x=-3
d: 9-3x=0
=>3x=9
hay x=3
e: -8-2x=0
=>-2x=8
hay x=-4
1 tháng 3 2022
a: 3(x-3)+4(x-2)=x-5
=>3x-9+4x-8=x-5
=>7x-17=x-5
=>6x=12
hay x=2
b: \(\Leftrightarrow x^2+2x-3x+9=x^2-7\)
=>9-x=-7
hay x=16
c: \(\Leftrightarrow x^2-x-2+3x-3-x^2+x=x-3\)
=>3x-5=-3
=>3x=2
hay x=2/3
d: \(\Leftrightarrow x^2-2x+1-x^2+4=3x-4\)
=>-2x+5=3x-4
=>-5x=-9
hay x=9/5
1 tháng 3 2022
a, \(3x-9+4x-8=x-5\Leftrightarrow6x=-5+17=12\Leftrightarrow x=2\)
b, \(x^2+2x-3x+9=x^2-7\Leftrightarrow-x=-16\Leftrightarrow x=16\)
c, \(x^2-x-2+3x-3-x^2+x=x-3\Leftrightarrow2x=2\Leftrightarrow x=1\)
d, \(x^2-2x+1-x^2+4=3x-4\Leftrightarrow-2x+5=3x-4\Leftrightarrow5x=9\Leftrightarrow x=\dfrac{9}{5}\)
e, \(x^2+4x+4+x^2-2x+1=2x^2-18\Leftrightarrow2x+5=-18\Leftrightarrow x=-\dfrac{23}{2}\)
1 tháng 3 2022
a: (x-3)(x+1)=0
=>x-3=0 hoặc x+1=0
=>x=3 hoặc x=-1
b: (2x-4)(6-2x)=0
=>2x-4=0 hoặc 6-2x=0
=>x=2 hoặc x=3
c: (x+3)(x-3)(3x-2)=0
nên \(x\in\left\{-3;3;\dfrac{2}{3}\right\}\)
24 tháng 4 2022
Mấy câu này dễ mà,đầu tiên bạn chia ra làm hai,bà trường hợp bằng dấu ngoặc vuông các trường hợp đó bạn sẽ để bằng 0 xong rồi bạn chỉ việc lấy những phân tử không có x để lấy 0 trừ hoặc cộng với những số đó ra kết quả như thế nào thì bạn sẽ lấy những số bạn vừa lấy 0 trừ hoặc cộng rồi bạn đem chia cho số có biến x
Vd:e)x(4x-2)(2x+3)=0
=>[x=0
[4x-2=0
[2x+3=0
<=>[x=0
[x=1/2
[x=-3/2
Vậy.....
30 tháng 10 2021
\(3,=x^2\left(x-2\right)+5\left(x-2\right)=\left(x^2+5\right)\left(x-2\right)\\ 6,=\left(x+y\right)^2-1=\left(x+y-1\right)\left(x+y+1\right)\\ 79,=25-\left(x+6\right)^2=\left(5-x-6\right)\left(5+x+6\right)=-\left(x+1\right)\left(x+11\right)\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
\(ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-2}{2}=1\)
Khi đó:
\(\text{VT}=\frac{a}{ab+bc+ac+a^2}+\frac{2b}{ab+bc+ac+b^2}+\frac{3c}{ab+bc+ac+c^2}\)
\(=\frac{a}{(a+b)(a+c)}+\frac{2b}{(b+a)(b+c)}+\frac{3c}{(c+a)(c+b)}\)
\(=\frac{a(b+c)+2b(a+c)+3c(a+b)}{(a+b)(b+c)(c+a)}\)
\(=\frac{3ab+4ac+5bc}{(a+b)(b+c)(c+a)}=\text{VP}\)
21 tháng 6 2023
a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
b: \(MP=\sqrt{PK\cdot PN}=10\left(cm\right)\)
1 tháng 3 2022
Bài 3:
a: 3(x-3)+4(x-2)=x-5
=>3x-9+4x-8=x-5
=>7x-17=x-5
=>6x=12
hay x=2
b: \(\Leftrightarrow x^2+2x-3x+9=x^2-7\)
=>9-x=-7
hay x=16
c: \(\Leftrightarrow x^2-x-2+3x-3-x^2+x=x-3\)
=>3x-5=-3
=>3x=2
hay x=2/3
d: \(\Leftrightarrow x^2-2x+1-x^2+4=3x-4\)
=>-2x+5=3x-4
=>-5x=-9
hay x=9/5
11 tháng 4 2022
Xét tam giác ABC và tam giác HBA, có:
^B: chung
^H=^A= 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA ( g.g ) ( 1 )
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=HB.BC\)
b.Xét tam giác ABC và tam giác HAC, có:
^C: chung
^A=^H = 90 độ
Vậy tam giác ABC đồng dạng tam giác HAC ( g.g ) ( 2 )
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Leftrightarrow AC^2=HC.BC\)
c.Bạn check lại đề
c. Từ (1) và (2) Suy ra: Tam giác HBA đồng dạng tam giác HAC
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\)
\(\Leftrightarrow AH^2=HB.HC\)
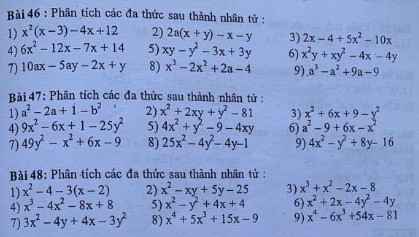
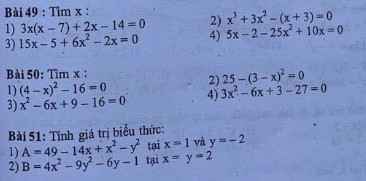
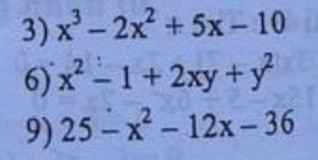
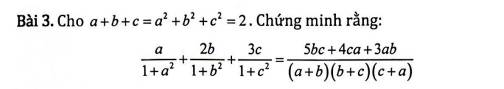
Tách ra đi bạn, dài quá
dài thế chỉ cần tách ra xong đặt phần chung rồi còn cái j nhét tất vào một ngoặc