
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Ta có:
\(f\left(x\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt: \(\left(x^2+5x+5\right)=a\) ta được:
\(=\left(a-1\right)\left(a+1\right)+1\)
\(=a^2-1+1=a^2\)
Thay lại \(a=\left(x^2+5x+5\right)\) được:
\(\left(x^2+5x+5\right)^2\)
- Đối chiếu với \(\left(ax^2+bx+c\right)^2\)
Vậy \(a=1;b=5;c=5\)

2: \(A=x^2-10x+25-34=\left(x-5\right)^2-34\ge-34\forall x\)
Dấu '=' xảu ra khi x=5
\(1,C=x^2+x-3\\ \Rightarrow C=\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{13}{4}\\ \Rightarrow C=\left(x+\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(C_{min}=-\dfrac{13}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
\(2,A=x^2-10x-9\\ \Rightarrow A=\left(x^2-10x+25\right)-34\\ \Rightarrow A=\left(x-5\right)^2-34\)
dấu "=" xảy ra \(\Leftrightarrow x=5\)
Vậy \(A_{min}=-34\Leftrightarrow x=5\)

3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54


c: \(C=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
=4xy
d: \(D=\left(\dfrac{x}{2}-y\right)\left(\dfrac{x}{2}+y\right)=\dfrac{1}{4}x^2-y^2\)

\(A=9x^2+4x=\left(9x^2+4x+\dfrac{4}{9}\right)-\dfrac{4}{9}=\left(3x+\dfrac{2}{3}\right)^2-\dfrac{4}{9}\ge-\dfrac{4}{9}\)
Vậy GTNN của A là \(-\dfrac{4}{9}\) khi x = \(-\dfrac{2}{9}\)
\(B=25x^2+x-1=\left(25x^2+x+\dfrac{1}{100}\right)-\dfrac{101}{100}=\left(5x+\dfrac{1}{10}\right)^2-\dfrac{101}{100}\ge-\dfrac{101}{100}\)
Vậy GTNN của B là \(-\dfrac{101}{100}\) khi x = \(-\dfrac{1}{50}\)
\(C=3x^2+4x+1=3\left(x^2+\dfrac{4}{3}x+\dfrac{4}{9}\right)-\dfrac{1}{3}=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{1}{3}\ge-\dfrac{1}{3}\)
Vậy GTNN của C là \(-\dfrac{1}{3}\) khi x = \(-\dfrac{2}{3}\)
 Mọi người cứu em, tối nay phải nộp rồi.
Mọi người cứu em, tối nay phải nộp rồi.

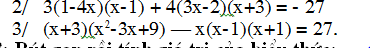



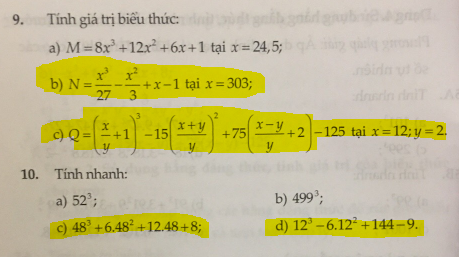 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 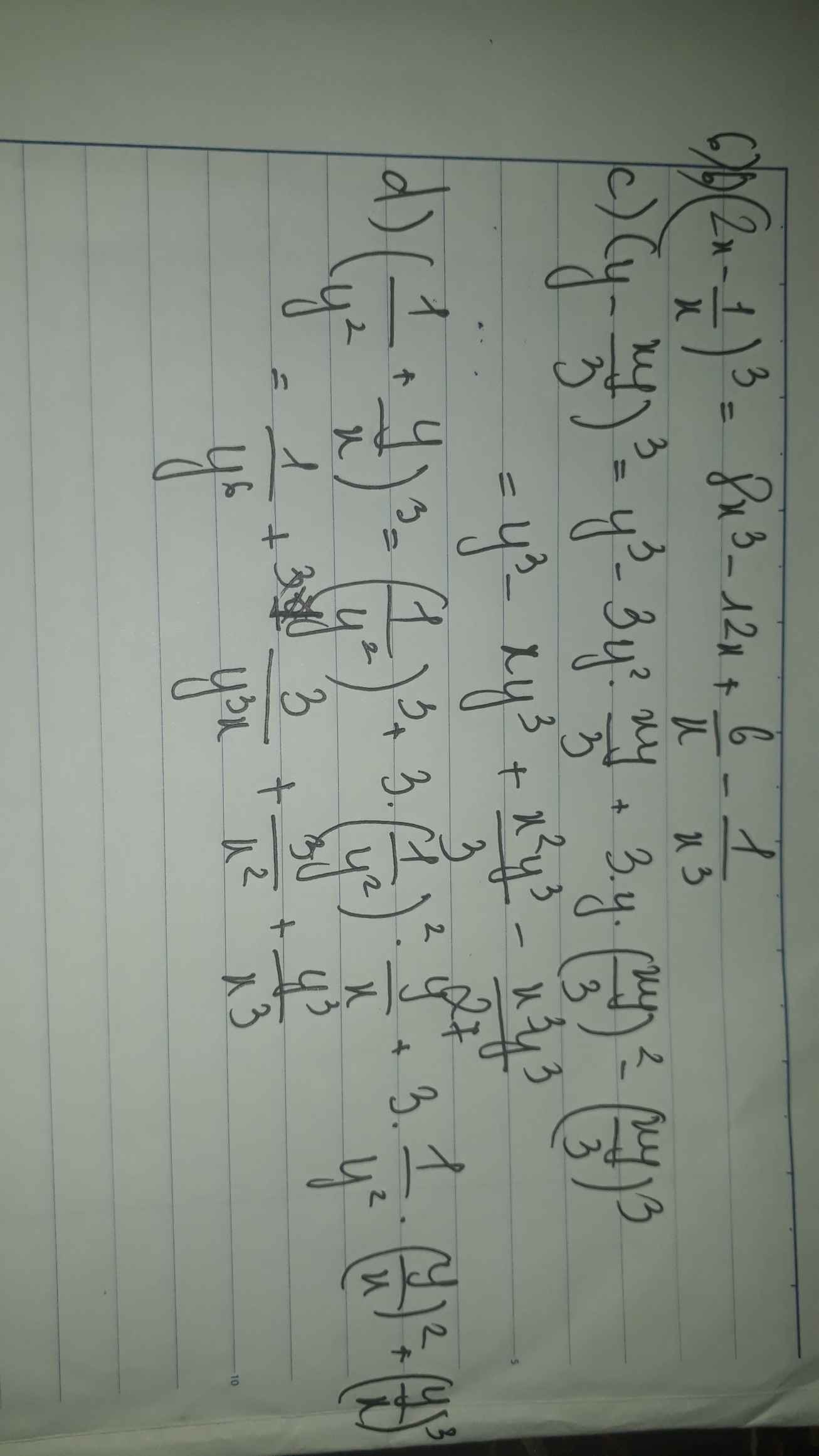
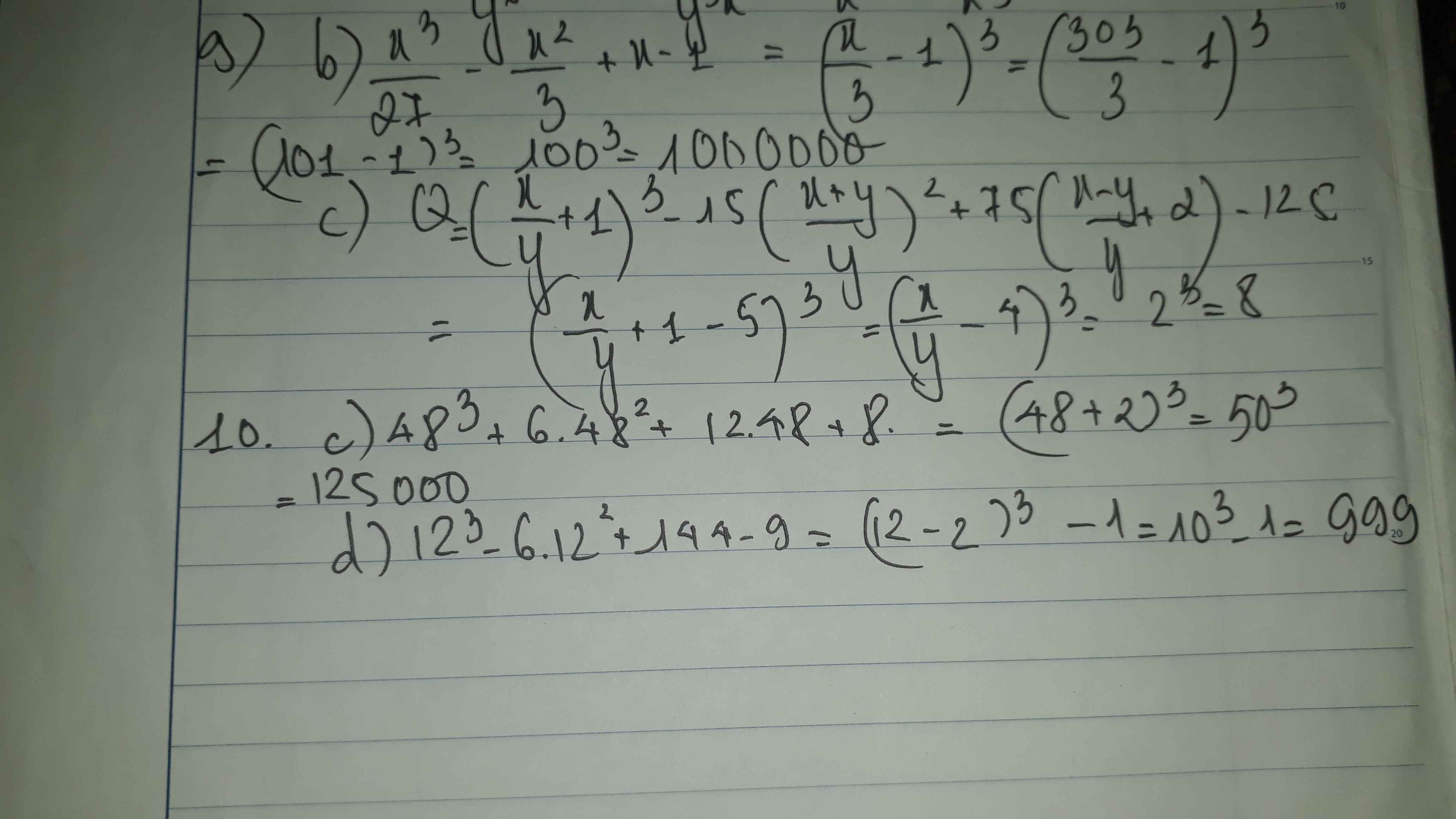
 Giúp em nhé mọi người mai phải nộp rồi
Giúp em nhé mọi người mai phải nộp rồi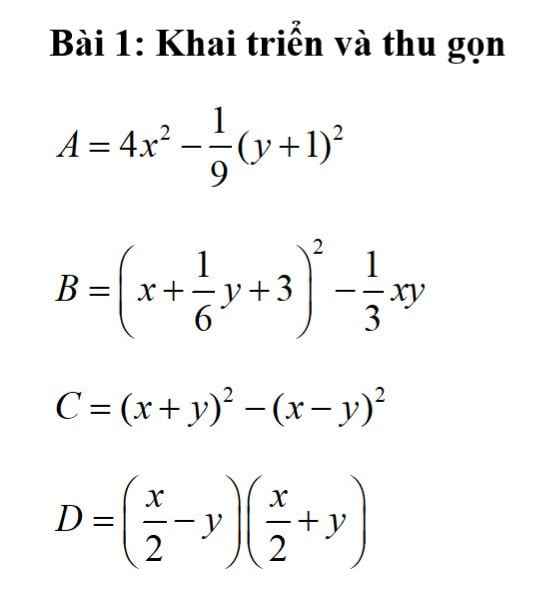
Bài 8:
a) Ta có: \(A=\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
b) Ta có: \(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3=8x^3\)