K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PD
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
1, \(x^2\) - \(x\) + \(\dfrac{1}{4}\) = 0
\(x^2\) - 2.\(x\).\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) = 0
(\(x\) - \(\dfrac{1}{2}\))2 = 0
\(x\) - \(\dfrac{1}{2}\) =0
\(x\) = \(\dfrac{1}{2}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
2, \(x^2\) - 10\(x\) = -25
\(x^2\) - 10\(x\) + 25 = 0
(\(x\) - 5)2 = 0
\(x\) - 5 =0
\(x\) = 5
25 tháng 7 2016
a) phép tính đã cho bằng 24x2y3z2 : (-6x2y2z2) +(-12x3y2z3) : (-6x2y2z2) + 36x2y2z2 : (-6x2y2z2) = -4y+2xz-6. Thế x,y,z vào rồi tính nha
câu b khi nãy mình giải ở dưới rồi :)
PD
2
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
2.26:
a. $x^2-6x+9-y^2=(x^2-6x+9)-y^2=(x-3)^2-y^2$
$=(x-3-y)(x-3+y)$
b. $4x^2-y^2+4y-4=4x^2-(y^2-4y+4)$
$=(2x)^2-(y-2)^2=(2x-y+2)(2x+y-2)$
c. $xy+z^2+xz+yz=(xy+xz)+(z^2+yz)=x(y+z)+z(z+y)$
$=(y+z)(x+z)$
c.
$x^2-4xy+4y^2+xz-2yz$
$=(x^2-4xy+4y^2)+(xz-2yz)$
$=(x-2y)^2+z(x-2y)=(x-2y)(x-2y+z)$
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
2.27:
a. $x^3+y^3+x+y=(x^3+y^3)+(x+y)$
$=(x+y)(x^2-xy+y^2)+(x+y)=(x+y(x^2-xy+y^2+1)$
b. $x^3-y^3+x-y=(x^3-y^3)+(x-y)=(x-y)(x^2+xy+y^2)+(x-y)$
$=(x-y)(x^2+xy+y^2+1)$
c.
$(x-y)^3+(x+y)^3=(x^3-3x^2y+3xy^2-y^3)+(x^3+3x^2y+3xy^2+y^3)$
$=2x^3+6xy^2=2x(x^2+3y^2)$
d.
$x^3-3x^2y+3xy^2-y^3+y^2-x^2$
$=(x^3-3x^2y+3xy^2-y^3)-(x^2-y^2)$
$=(x-y)^3-(x-y)(x+y)=(x-y)[(x-y)^2-(x+y)]$
$=(x-y)(x^2-2xy+y^2-x-y)$
2 tháng 10 2021
a: Xét ΔAHD có
AP là đường cao ứng với cạnh HD
AP là đường trung tuyến ứng với cạnh HD
Do đó: ΔAHD cân tại A
mà AP là đường cao ứng với cạnh HD
nên AP là đường phân giác ứng với cạnh HD
Xét ΔAHE có
AQ là đường cao ứng với cạnh HE
AQ là đường trung tuyến ứng với cạnh HE
Do đó: ΔHAE cân tại A
mà AQ là đường cao ứng với cạnh HE
nên AQ là đường phân giác ứng với cạnh HE
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của DE
2 tháng 10 2021
a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)
góc APD = APH=90o
AD = AH
AP chung
=> AD=AH (1)
CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)
=> AE= AH (2)
Từ 1 và 2 => AD= AE
=> A là trung điểm của DE
b) Xét \(\Delta DHE\) có:
DP=PH; HQ=QE
=> PQ là đg trung bình của tam giắc DHE
=> PQ// DE; PQ=1/2 DE
c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o
=> Tứ giác APHQ là HCN
=> PQ=AH ( theo t/c HCN)
B
4
17 tháng 9 2023
\(\left\{{}\begin{matrix}x+y=1\\xy=-1\end{matrix}\right.\)
\(F=x^8+y^8\)
\(\Leftrightarrow F=\left(x^4+y^4\right)^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left[\left(x^2+y^2\right)^2-2\left(xy\right)^2\right]^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left\{\left[\left(\left(x+y\right)^2-2xy\right)^2-2\left(xy\right)\right]^2\right\}^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left\{\left[\left(\left(1\right)^2-2.\left(-1\right)\right)^2-2\left(-1\right)^2\right]\right\}^2-2\left(-1\right)^4\)
\(\Leftrightarrow F=\left\{\left[9-2\right]\right\}^2-2=49-2=47\)
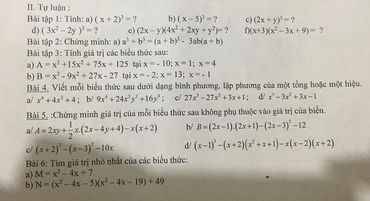
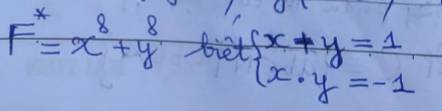
Bài `1`
`a, (x+2)^2 =x^2 +4x+4`
`b, (x-5)^2=x^2 -10x+25`
`c,(2x-y)^2=(2x)^2- 2*2x*y+y^2=4x^2-4xy+y^2`
`d,(3x^2-2y)^2= (3x^2)^2 - 2*3x^2*2y +(2y)^2=9x^4-12x^2y +4y^2`
`e,,(2x-y)(4x^2+2xy+y^2)= (2x)^3-y^3=8x^3-y^3`
`f,(x+3)(x^2-3x+9)=x^3+3^3=x^3+27`