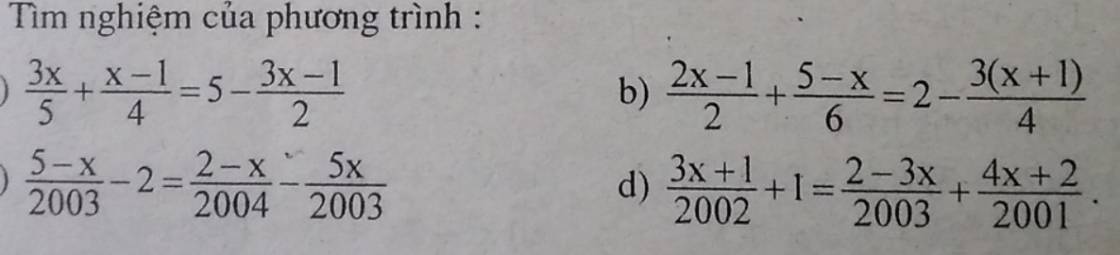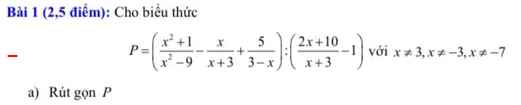K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2021
\(a,BD=\sqrt{AB^2+AD^2}=\sqrt{5^2+12^2}=13\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BD\\AD^2=DH\cdot BD\\AH^2=BH\cdot HD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BD}=\dfrac{25}{13}\left(cm\right)\\DH=\dfrac{AD^2}{BD}=\dfrac{144}{13}\left(cm\right)\\AH=\sqrt{\dfrac{25\cdot144}{13^2}}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
\(b,\widehat{MAN}=\widehat{ANM}=\widehat{AMN}\left(=90^0\right)\\ \Rightarrow AMHN.là.hcn\\ \Rightarrow AH=MN=\dfrac{60}{13}\left(cm\right)\)
\(c,\) Vì \(AMHN\) là hcn nên \(\widehat{MAH}=\widehat{ANM}\)
Mà \(\widehat{MAH}=\widehat{ADB}\left(cùng.phụ.\widehat{HAD}\right)\)
\(\Rightarrow\widehat{ANM}=\widehat{ADB}\)
\(\left\{{}\begin{matrix}\widehat{ANM}=\widehat{ADB}\\\widehat{BAD}.chung\end{matrix}\right.\Rightarrow\Delta AMN\sim\Delta ADB\left(g.g\right)\\ \Rightarrow\dfrac{AM}{AD}=\dfrac{AN}{AB}\Rightarrow AM\cdot AB=AN\cdot AD\)
TM
17 tháng 9 2021
a/ Xét △AHB và △DAB ta được: △AHB đồng dạng △DAB (g.g) (Tự chứng minh)
\(\Rightarrow\dfrac{AH}{AD}=\dfrac{HB}{AB}=\dfrac{AB}{BD}\left(a\right)\)
Áp dụng định lí Pytago vào △ADB được: \(BD=\sqrt{12^2+5^2}=13\left(cm\right)\). Thay vào (a) được:
\(\dfrac{AH}{AD}=\dfrac{HB}{AB}=\dfrac{AB}{13}\) hay \(\dfrac{AH}{12}=\dfrac{HB}{5}=\dfrac{5}{13}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{5.12}{13}\approx4,62\left(cm\right)\\HB=\dfrac{5^2}{13}\approx1,92\left(cm\right)\\HD=13-1,92=11,08\left(cm\right)\end{matrix}\right.\)
==========
b/ \(\begin{matrix}\hat{A}=90\text{°}\\\hat{AMH}=90\text{°}\\\hat{ANH}=90\text{°}\end{matrix}\) ⇒ AMHN là hình chữ nhật ⇒ \(AH=MN\approx4,92\left(cm\right)\)
==========
c/ Ta có: △AMN = △HNA (c.g.c) (Tự chứng minh)
Ta cũng có: △HNA đồng dạng △AHB (g.g) (Tự chứng minh) ⇒ △HNA đồng dạng △DAB (cùng đồng dạng △AHB) ⇒ △AMN đồng dạng △DAB
Vậy: \(\dfrac{AM}{AN}=\dfrac{AB}{AD}\) hay \(AM.AD=AN.AB\left(đpcm\right)\)
7 tháng 11 2021
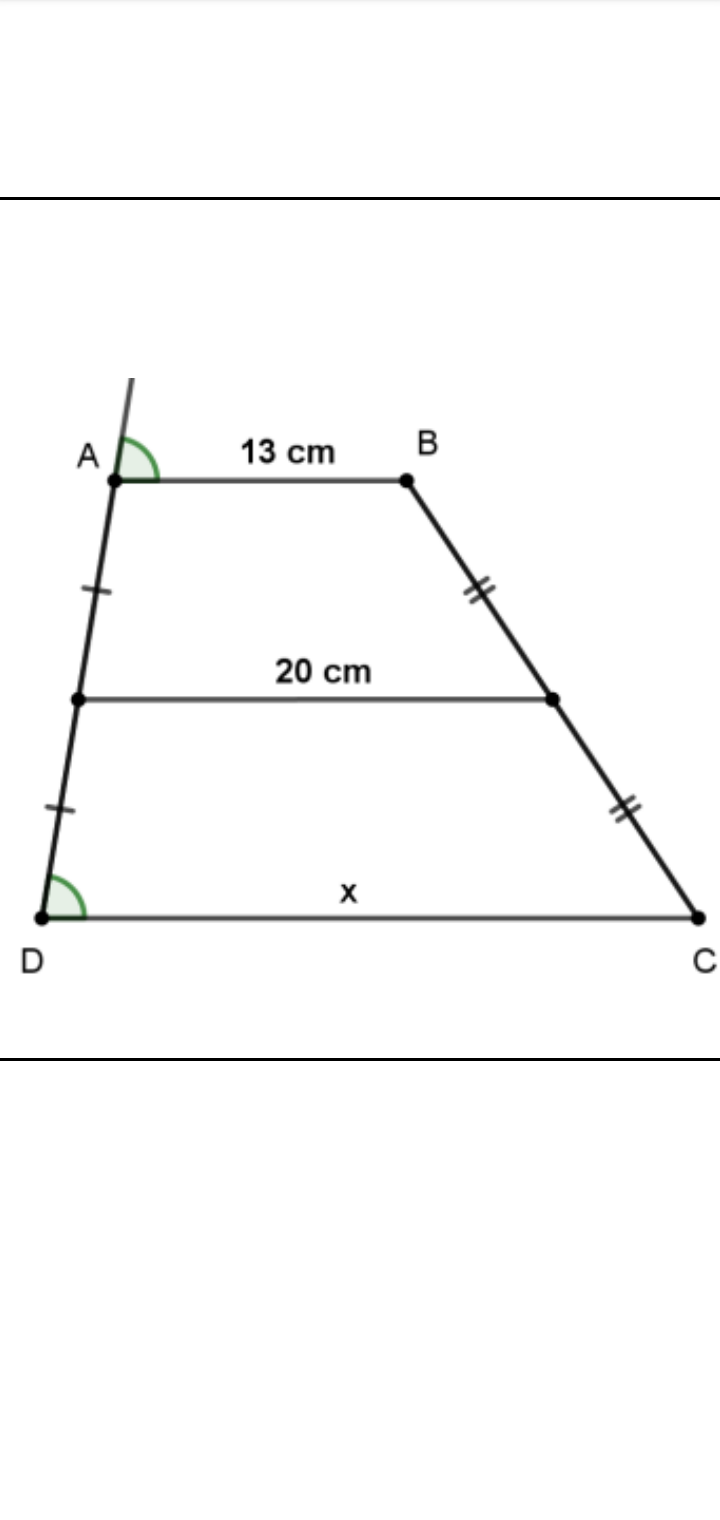
nếu tìm x thì:
ta có: (x+13):2=20
x+13=40
x=27(cm)
vậy x=17cm
11 tháng 9 2021
\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\cdot\left(-2ab\right)+6a^2b^2\)
\(=1-3ab-6a^2b^2+6a^2b^2\)
\(=1-3ab\)
6 tháng 11 2021
Vì tổng các góc của hình tứ giác là 360o
Nên 3x + 5x + 2x +60o = 360o
\(\Rightarrow x=30^o\)
6 tháng 11 2021
\(10x=300\)
nên x=30
=>\(\widehat{A}=150^0;\widehat{B}=90^0;\widehat{D}=60^0\)
18 tháng 2 2023
a: \(\Leftrightarrow20\left(5x-5+2\right)-15\left(9x-1\right)=24\left(3x+1\right)-60\)
\(\Leftrightarrow100x-60-135x+15=72x+24-60\)
=>72x-36=-35x-45
=>107x=-9
=>x=-9/107
b: \(\Leftrightarrow15\left(x-2\right)+2\left(5x-9.5\right)=16\left(x+2\right)+100\)
=>15x-30+10x-19=16x+32+100
=>25x-49=16x+132
=>9x=181
=>x=181/9
c: \(\Leftrightarrow3\left(9x+3+2\right)-18=4\left(5x+1\right)-3x-1\)
=>3(9x+5)-18=20x+4-3x-1=17x+3
=>27x+15-18=17x+3
=>10x=3-15+18=6
=>x=3/5
d: \(\Leftrightarrow8x+4+9\left(4x+1\right)=2\left(3x+2x+2\right)+11x+5\)
=>8x+4+36x+9=10x+4+11x+5
=>44x+13=21x+9
=>23x=-4
=>x=-4/23
T
1
19 tháng 2 2023
a: =>12x+5(x-1)=100-10(3x-1)
=>12x+5x-5=100-30x+30
=>17x-5=-30x+130
=>47x=135
=>x=135/47
b: \(\Leftrightarrow6\left(2x-1\right)+2\left(5-x\right)=24-9\left(x+1\right)\)
=>12x-6+10-2x=24-9x-9
=>10x+4=-9x+15
=>19x=11
=>x=11/19
6 tháng 3 2022
\(P=\left(\dfrac{x^2+1}{x^2-9}-\dfrac{x}{x+3}+\dfrac{5}{3-x}\right):\left(\dfrac{2x+10}{x+3}-1\right)\)
\(=\left(\dfrac{x^2+1}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{5\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10}{x+3}-\dfrac{x+3}{x+3}\right)\)
\(=\left(\dfrac{x^2+1-x^2+3x-5x-15}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\left(\dfrac{-2x-14}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{x+7}{x+3}\right)\)
\(=\dfrac{-2\left(x+7\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{x+7}\)
\(=\dfrac{-2}{x-3}\)
6 tháng 3 2022
đk : x khác -3 ; 3 ; -7
\(P=\left(\dfrac{x^2+1+x\left(x-3\right)+5x+15}{x^2-9}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\dfrac{2x^2+1+2x+15}{x^2-9}:\dfrac{x+7}{x+3}=\dfrac{2x^2+2x+16}{\left(x-3\right)\left(x+7\right)}\)
MN
1
9 tháng 11 2021
a: Xét tứ giác HMKN có
I là trung điểm của HK
I là trung điểm của MN
Do đó: HMKN là hình bình hành