K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KC
2
2 tháng 3 2022
\(ĐK:x\ne0\)
\(\dfrac{x-1}{3}+\dfrac{x+3}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x-1\right)+3\left(x+3\right)}{3x}=\dfrac{6x}{3x}\)
\(\Leftrightarrow x\left(x-1\right)+3\left(x+3\right)=6x\)
\(\Leftrightarrow x^2-x+3x+9-6x=0\)
\(\Leftrightarrow x^2-4x+9=0\)
Ta có: \(x^2-4x+9=x^2-4x+4+5=\left(x-2\right)^2+5\ge5>0\)
Vậy pt vô nghiệm
4 tháng 1 2023
a: ĐKXĐ: x<>0; x<>1(A)
(B): x<>0; x<>3
(C): x<>2; x<>-2
b: \(A=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(B=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(C=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
c: Khi x=0 thì A và B không xác định
Khi x=0 thì C=3/2
Khi x=3 thì B ko xác định, A=2/3; C=3/5
Y
4 tháng 1 2023
\(a,DKXD:\)
\(+x^2-x\ne0\Leftrightarrow x\ne0;1\)
\(+x^2-3x\ne0\Leftrightarrow x\ne0;3\)
+\(x^2-4\ne0\Leftrightarrow x\ne\pm4\)
\(b,\)
\(\dfrac{2x-2}{x^2-x}=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)
\(\dfrac{2x-6}{x^2-3x}=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)
\(\dfrac{3x-6}{x^2-4}=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)
\(c,\)
Vì phân thức 1,2 cùng kết quả nên mk lm 1 cái thôi nhé
+ Thay \(x=0\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{0}=0\)
Thay \(x=3\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{3}\)
+ Thay \(x=0\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{0+2}=\dfrac{3}{2}\)
Thay \(x=3\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{3+2}=\dfrac{3}{5}\)
GH
12 tháng 7 2023
1
Với \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\)
\(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\left(\dfrac{x^2+2x+1}{4x^4-4x^2+1}\right)\\ =\left(\dfrac{\left(x-1\right)\left(x+1\right)}{\left(2-x\right)\left(x+1\right)}+\dfrac{x^2}{\left(x+1\right)\left(2-x\right)}\right)\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{x^2-1+x^2}{\left(x+1\right)\left(2-x\right)}\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{\left(2x^2-1\right)\left(x+1\right)^2}{\left(x+1\right)\left(2-x\right)\left(2x^2-1\right)^2}\\ =\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}\)
2
Để M = 0 thì \(\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}=0\Rightarrow x+1=0\Rightarrow x=-1\) (loại)
Vậy không có giá trị x thỏa mãn M = 0
H9
HT.Phong (9A5)
CTVHS
12 tháng 7 2023
1) \(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\cdot\dfrac{x^2+2x+1}{4x^4-4x^2+1}\) (ĐK: \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\))
\(M=\left(\dfrac{-\left(x-1\right)}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x^2-1\right)-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-2x^2+1}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(2x^2-1\right)\left(x+1\right)^2}{\left(x-2\right)\left(x+1\right)\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}\)
2) Ta có: \(M=0\)
\(\Rightarrow\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}=0\)
\(\Leftrightarrow-\left(x+1\right)=0\)
\(\Leftrightarrow-x=1\)
\(\Leftrightarrow x=-1\left(ktm\right)\)
L
1
28 tháng 10 2021
bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu
NT
1
10 tháng 3 2022
\(a)P=\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\right).\left(\dfrac{x^2}{x+1}+1\right).\left(x\ne1;x\ne-1\right).\\ P=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}.\dfrac{x^2+x+1}{x+1}.\\ P=\dfrac{x^2-x}{x-1}.\dfrac{1}{x+1}.\\ P=\dfrac{x\left(x-1\right)}{x-1}.\dfrac{1}{x+1}.\\ P=x.\dfrac{1}{x+1}.\\ P=\dfrac{x}{x+1}.\)
\(P=\dfrac{1}{4}.\Rightarrow\dfrac{x}{x+1}=\dfrac{1}{4}.\\ \Leftrightarrow4x-x-1=0.\\ \Leftrightarrow3x-1=0.\\ \Leftrightarrow x=\dfrac{1}{3}\left(TM\right).\)
MN
1
9 tháng 11 2021
a: Xét tứ giác HMKN có
I là trung điểm của HK
I là trung điểm của MN
Do đó: HMKN là hình bình hành
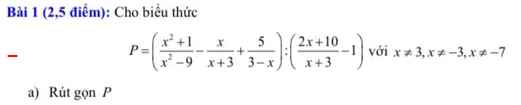
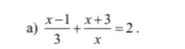
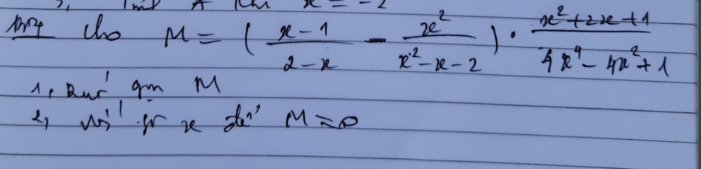
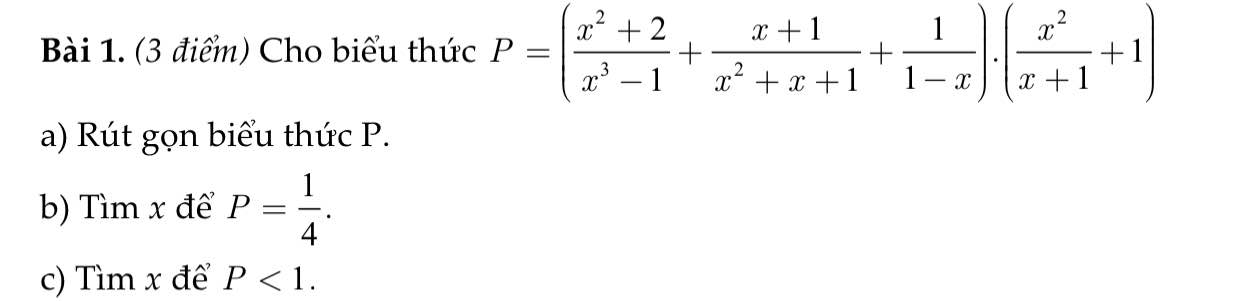
\(P=\left(\dfrac{x^2+1}{x^2-9}-\dfrac{x}{x+3}+\dfrac{5}{3-x}\right):\left(\dfrac{2x+10}{x+3}-1\right)\)
\(=\left(\dfrac{x^2+1}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{5\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10}{x+3}-\dfrac{x+3}{x+3}\right)\)
\(=\left(\dfrac{x^2+1-x^2+3x-5x-15}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\left(\dfrac{-2x-14}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{x+7}{x+3}\right)\)
\(=\dfrac{-2\left(x+7\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{x+7}\)
\(=\dfrac{-2}{x-3}\)
đk : x khác -3 ; 3 ; -7
\(P=\left(\dfrac{x^2+1+x\left(x-3\right)+5x+15}{x^2-9}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\dfrac{2x^2+1+2x+15}{x^2-9}:\dfrac{x+7}{x+3}=\dfrac{2x^2+2x+16}{\left(x-3\right)\left(x+7\right)}\)