Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn ông viết mũ nhá =) Ông hãy nhìn bên trên phần mình đăng bài + trả lời . Bẹn có thể thấy các kí tự khó hiểu vl :v Như : Hình ảnh , Tex , ... Hãy nhìn X2 và X2 ấn vô đó , lak ấn đc :VVV
#Mật

GTNN (A)=3178+2017 khi x=0 ko co GTLN
GTLN(b)=2017 khi x=-3 va y=5 khong co GTNN
GTNN(c)=2018 khi x=-1 va y=5 khong co GTLN
neu can giai thich thi h
ko thi thoi
em cũng muốn làm phước giúp chị lắm chứ nhưng em mới ở lớp 6 thui


Ở đây dấu * mik vẽ trong fx là như vầy \(\circledast\)
Xét phép trừ thứ hai: \(\overline{\circledast\circledast\circledast}-\overline{\circledast\circledast}=\circledast\) suy ra số bị trừ có dạng \(\overline{10\circledast}\), do đó bằng 100 (vì chữ số đơn vị của số bị trừ là chữ số 0 thêm vào để tìm các chữ số thập phân của thương).
Đặt số chia, thương và tích riêng thứ nhất theo thứ tự là \(\overline{ab};\overline{c,deg};\overline{mn}.\)
Ta thấy 10: \(\overline{ab}=\overline{0,deg}\) nên \(10000=\overline{ab}.\overline{deg}.\)
Chú ý rằng \(d\ne0\) (vì nếu d = 0 thì \(\overline{ab}.\overline{eg}< 10000\) ), \(g\ne0\) (vì nếu g = 0 thì thương đã dừng lại ở e), \(\overline{deg}\) là ước của 10 000 và có ba chữ số. Suy ra \(\overline{deg}\) bằng 53 =125 hoặc 54 = 625. Tương ứng \(\overline{ab}=80\) hoặc 16.

Trường hợp \(\overline{ab}=80\) thì \(\overline{mn}=80\), trái với \(80+10=\circledast\circledast\circledast\) (số bị chia), loại.
Trường hợp \(\overline{ab}=16\) thì \(c=6,\overline{mn}=96,\) số bị chia là 96 + 10 = 106
Ta có: \(106:16=6,625\) và 

Bài 13:
a: Xét ΔAIB có \(\widehat{AIC}\) là góc ngoài tại đỉnh I
nên \(\widehat{AIC}=\widehat{ABI}+\widehat{BAI}=60^0+\widehat{BAI}\)
=>\(\widehat{AIC}>60^0\)
b: Ta có: \(\widehat{AIC}>60^0\)
\(\widehat{ACI}=60^0\)
Do đó: \(\widehat{AIC}>\widehat{ACI}\)
Xét ΔAIC có \(\widehat{AIC}>\widehat{ACI}\)
mà AC,AI lần lượt là các cạnh đối diện của các góc AIC và ACI
nên AC>AI
3: Vì I nằm giữa B và C nên tia AI nằm giữa hai tia AB và AC
=>\(\widehat{BAI}+\widehat{CAI}=\widehat{BAC}\)
=>\(\widehat{BAI}+\widehat{CAI}=60^0\)
=>\(\widehat{CAI}< 60^0\)
=>\(\widehat{CAI}< \widehat{ACI}< \widehat{AIC}\)
Xét ΔACI có \(\widehat{CAI}< \widehat{ACI}< \widehat{AIC}\)
mà CI,AI,AC lần lượt là các cạnh đối diện của các góc CAI;ACI;AIC
nên CI<AI<AC
Bài 12:
a: Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{ACD}\)
=>\(\widehat{ADB}=60^0+\widehat{DAC}\)
=>\(\widehat{ADB}>60^0\)
b: Xét ΔADB có \(\widehat{ADB}>\widehat{ABD}\)
mà AB,AD là các cạnh đối diện của các góc ADB,ABD
nên AB>AD
mà AB=AC
nên AC>AD
3: Vì D nằm giữa B và C nên tia AD nằm giữa hai tia AB và AC
=>\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)
=>\(\widehat{BAD}+\widehat{CAD}=60^0\)
=>\(\widehat{BAD}< 60^0\)
=>\(\widehat{BAD}< \widehat{ABD}< \widehat{ADB}\)
Xét ΔBAD có \(\widehat{BAD}< \widehat{ABD}< \widehat{ADB}\)
mà BD,AD,AB là các cạnh đối diện của các góc BAD;ABD;ADB
nên BD<AD<AB



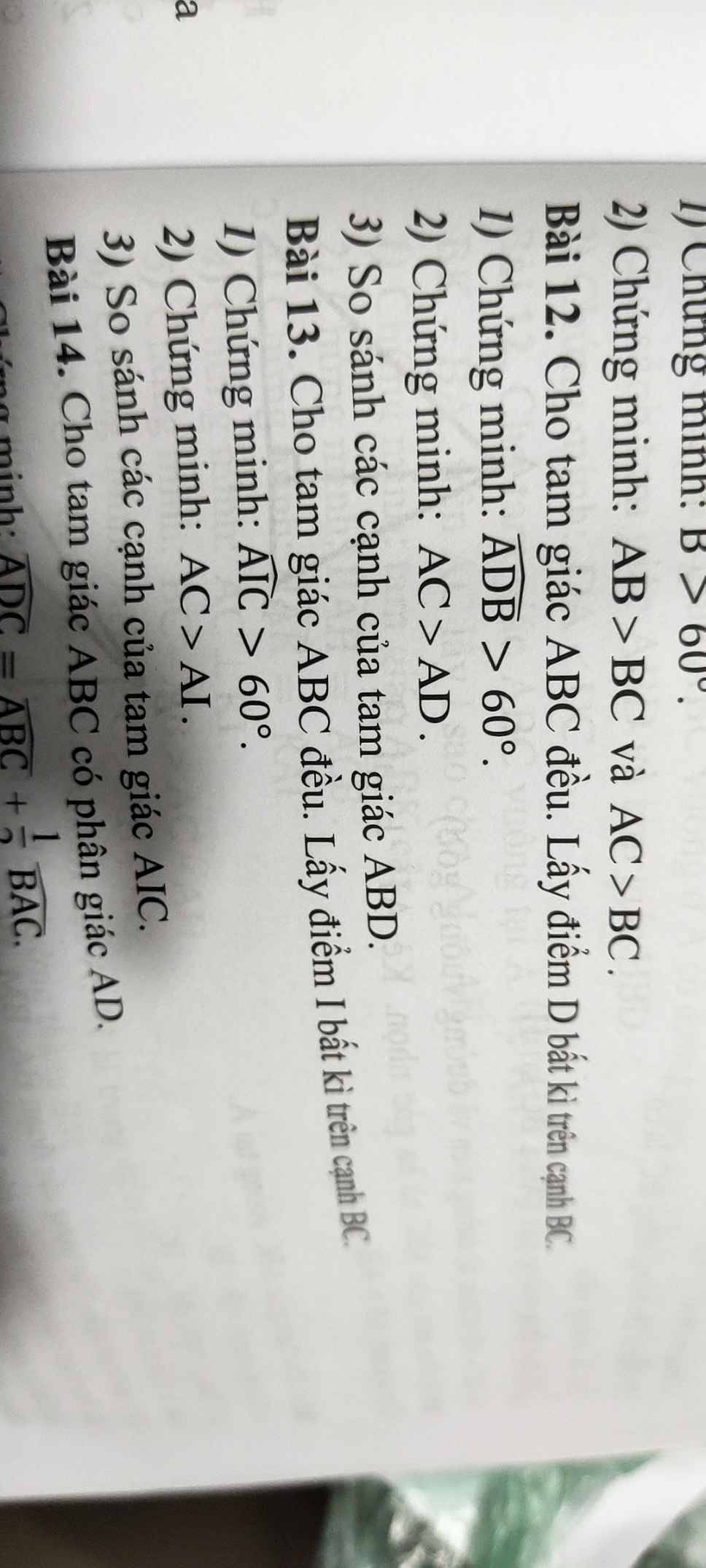


thử cách này xem (ko chắc đúng đâu vì nó ko sử dụng hết giả thiết bài toán)
Gọi giao điểm của AB và DC là K.
Khi đó ta có BK // DE suy ra ^BKD = ^KDE = 133o. Suy ra ^BKC = 180o - 133 = 47o. Mặt khác ta có AB và BK là hai tia đổi nhau (do cách dựng) nên ^ABC và ^KBC kề bù suy ra ^KBC = 180 - 120 = 60o
Áp dụng định lí tổng 3 góc trong một tam giác suy ra:
^BCD + ^KBC + ^BKC = 180o
Hay ^BCD + 60o + 47o = 180o
Suy ra ^BCD = 73o
đề troll người à? 20 độ là cái góc nào thế???