
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a² + b² + c² + d² + e² ≥ a(b + c + d + e)
Ta có: a² + b² + c² + d² + e²
= (a²/4 + b²) + (a²/4 + c²) + (a²/4 + d²) + (a²/4 + e²)
Lại có: (a/2 - b)² ≥ 0 <=> a²/4 - ab + b² ≥ 0 <=> a²/4 + b² ≥ ab
Tương tự ta có:
. a²/4 + c² ≥ ac
. a²/4 + d² ≥ ad
. a²/4 + e² ≥ ae
--> (a²/4 + b²) + (a²/4 + c²) + (a²/4 + d²) + (a²/4 + e²) ≥ ab + ac + ad + ae
<=> a² + b² + c² + d² + e² ≥ a(b + c + d + e) --> đ.p.c.m
Dấu " = " xảy ra <=> a/2 = b = c = d = e
P/s: Hơi hơi dễ nhỉ

d) Tự vẽ hình nhé
Dễ thấy I là trực tâm => CK là đường cao.
Do AM là phân giác nên góc MAB = góc MAC = 45
mà góc MAB = góc ICB
suy ra góc KBC = 45
=> góc BDM = 45
=> MB = MD (do tam giác MBD vuông cân)
Do AM là phân giác nên ta có tỷ lệ sau \(\frac{MC}{6}=\frac{MB}{8}\)
Theo Pythagoras => (MC + MB)^2 = AC^2 + AB^2 = 100
Áp dụng tính chất dãy tỉ số bằng nhau , suy ra
\(\frac{MC}{6}=\frac{MB}{8}=\frac{MC+MB}{14}=\frac{10}{14}=\frac{5}{7}\)
=> \(\hept{\begin{cases}MC=\frac{30}{7}\\MB=\frac{40}{7}\end{cases}}\)
Suy ra \(MD=\frac{40}{7}\)
Suy ra \(S_{BCD}=\frac{1}{2}.MD.BC=\frac{1}{2}.\frac{40}{7}.10=\frac{200}{7}\)
Ta áp dụng Pythgoras vào tam giác CMD để tính CD = 50/7
Sau đó tinh S(CMA) dựa vào tỷ lệ
Rồi lấy S(BCD) - S(CMA) là ra S(BMAD)

b: Xét hình thang MNEK có
A là trung điểm của MK
AB//MN//EK
Do đó: B là trung điểm của NE
Suy ra: x=5cm
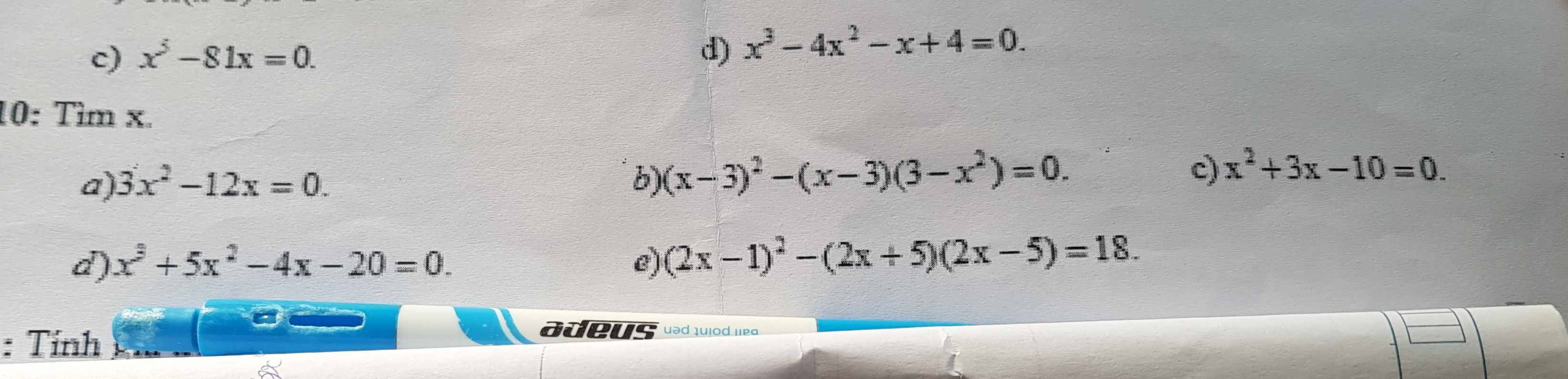
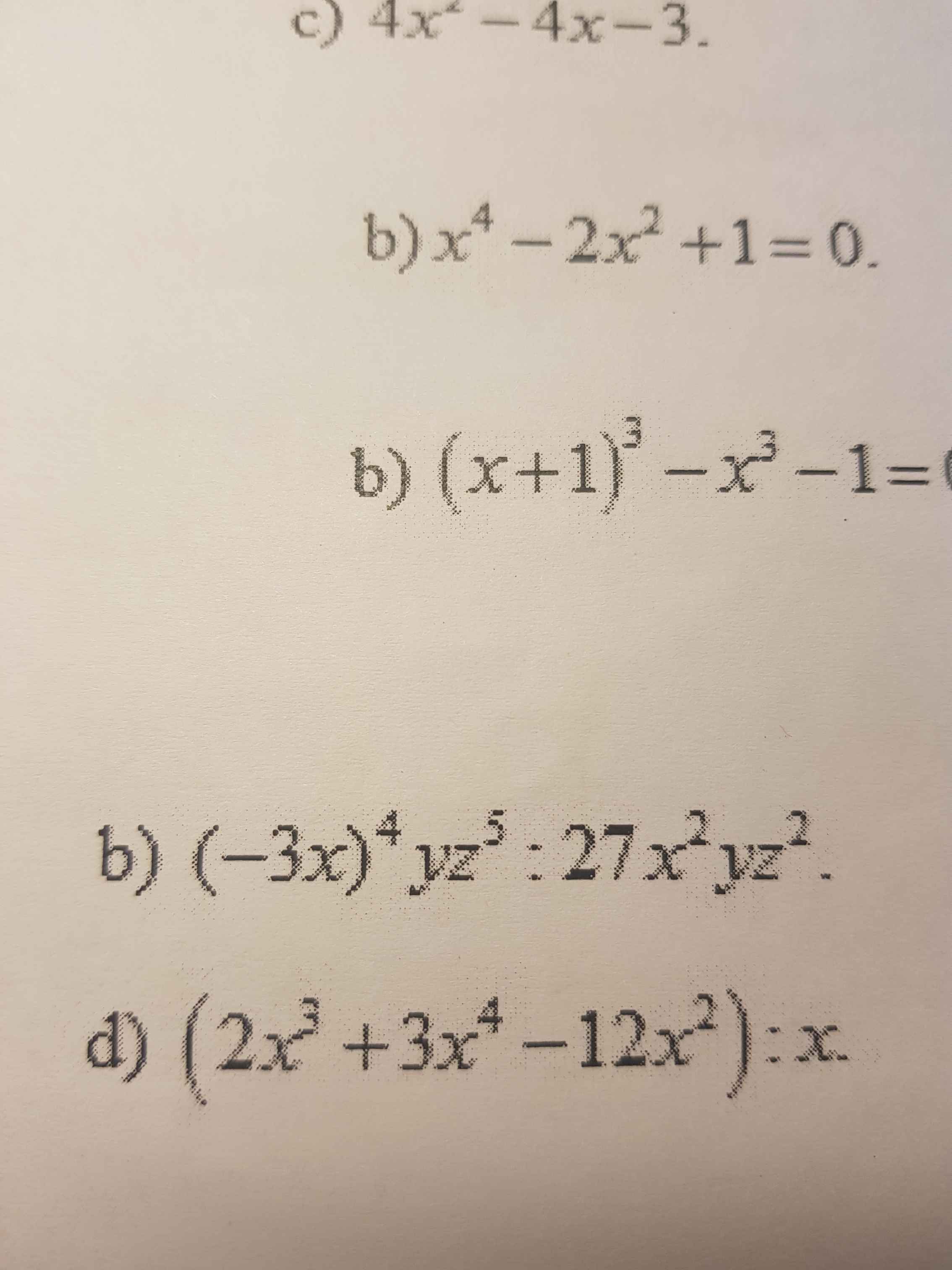


 lm hộ em vs ạ
lm hộ em vs ạ
a) \(\Rightarrow3x\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b) \(\Rightarrow\left(x-3\right)\left(x-3-3+x^2\right)=0\Rightarrow\left(x-3\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-3\end{matrix}\right.\)
c) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x+5\right)-4\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x+5\right)\left(x-2\right)\left(x+2\right)=0\)\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\\x=-2\end{matrix}\right.\)
e) \(\Rightarrow4x^2-4x+1-4x^2+25=18\)
\(\Rightarrow4x=8\Rightarrow x=2\)
10.
b) \(\Leftrightarrow\left(x-3\right)\left(x-3-3+x^2\right)=0\\ \Leftrightarrow\Leftrightarrow\left(x-3\right)\left(x^2+x-6\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-3\end{matrix}\right.\)
d) \(\Leftrightarrow x^2\left(x+5\right)-4\left(x+5\right)=0\\ \Leftrightarrow\left(x+5\right)\left(x^2-4\right)=0\\ \Leftrightarrow\left(x+5\right)\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\\x=-2\end{matrix}\right.\)
e) \(\Leftrightarrow4x^2-4x+1-4x^2+25-18=0\\ \Leftrightarrow-4x+8=0\\ \Leftrightarrow x=2\)