Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có số có 2018 chữ số lớn nhất là 999....99 (2018 chữ số 9)
=> A lỡn nhất là 2018 x 9 = 18162
=> B lớn nhất là 1 + 8 + 1 + 6 + 2 = 18
=> C lớn nhất là 1 + 8 = 9
Ta có 3 x 9 + 2 = 29 mà 29 là số nguyên tố nên không tồn tại số như vậy

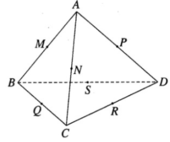
Giả sử có một mặt cầu tiếp xúc với các cạnh AB, AC, AD, BC, CD, BD của tứ diện ABCD lần lượt tại M, N, P, Q, R, S. Khi đó AM, AN, AP là các tiếp tuyến cùng xuất phát từ A nên AM = AN = AP.
Lập luận tương tự ta có: BM = BQ = BS; CQ = CR = CN; DR = DS = DP
Vậy AB + CD = AM + MB + CR + RD = AN + BS + CN + DS = AN + NC + BS + SD = AC + BD
Bằng lí luận tương tự ta chứng minh được AB + CD = AC + BD = AD + BC

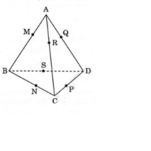
Gọi mặt cầu S(O; R) tiếp xúc với các cạnh của hình tứ diện đã cho lần lượt tại M, N, P, Q ,R và S.
* Ta chứng minh: AM = AR = AQ.
Do mặt cầu tiếp xúc với ba cạnh AB, AC và AD lần lượt tại M; R và Q nên :
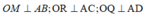
Xét ba tam giác OAM; OAR và OAQ có:
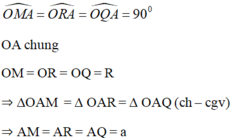
* Chứng minh tương tự ta có:
BM = BN = BS = b
CP = CN = CR = c.
DP = DQ = DS = d
Ta có:
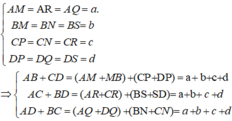
Do đó, AB + CD = AC + BD = AD + BC.

Gọi M 1 là một mặt của hình đa diện (H). Gọi A, B, C là ba đỉnh liên tiếp của M 1 . Khi đó AB, BC là hai cạnh của (H). Gọi M 2 là mặt khác với M 1 và có chung cạnh AB với M 1 . Khi đó M 2 còn có ít nhất một đỉnh D khác với A và B. Nếu D ≡ C thì M 1 và M 2 có hai cạnh chung AB và BC, điều này vô lý. Vậy D phải khác C. Do đó (H) có ít nhất bốn đỉnh A, B, C, D.

Gọi \(M_1\) là một mặt của hình đa diện (H). Gọi A, B, C là đỉnh liên tiếp của \(M_1\). Khi đó AB, BC là hai cạnh của (H). Gọi \(M_2\) làm mặt khác với \(M_1\) và có chung cạnh AB với \(M_1\). Khi đó \(M_2\) còn có ít nhất một đỉnh D khác với A và B. Nếu \(D\equiv C\) thì \(M_1\) và \(M_2\) có hai cạnh chung AB và BC, điều này vô lí.
Vậy D phải khác C. Do đó (H) có ít nhất bốn đỉnh A, B, C, D

Chọn B
Tập xác định D = ℝ \{1}
Ta có 
Do đó hàm số nghịch biến trên đoạn [2;3]
Suy ra ![]()
Vậy có 1 giá trị nguyên dương của m.


hhbgdycnwehew5hwjeu6jpt2omctjmwejvicku[4to
dddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddd