Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Gọi số tiền ông Sáu gửi ban đầu là x.
Theo đề bài ta có:
Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)
Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)
Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)
Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)
Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng
Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.
Tổng % lãi suất trong 2 năm là :
6% . 2 = 12%
Số tiền lãi trong 2 năm là :
112360000 . 12% = 13483200
=> Tiền ông Sáu gửi là :
112360000 - 13483200 = 98876800

Cách 1:
Gọi x là số tiền mua trái phiếu chính phủ và y là số tiền mua trái phiếu ngân hàng. (đơn vị triệu đồng) (\(x,y \le 1200\))
Khi đó, số tiền mua trái phiếu doanh nghiệp là \(1200 - x - y\)(triệu đồng)
Vì số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên \(x \ge 3y\)
Vì bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(1200 - x - y \le 200 \Leftrightarrow x + y \ge 1000\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Biểu diễn miền nghiệm của hệ trong mp tọa độ ta được
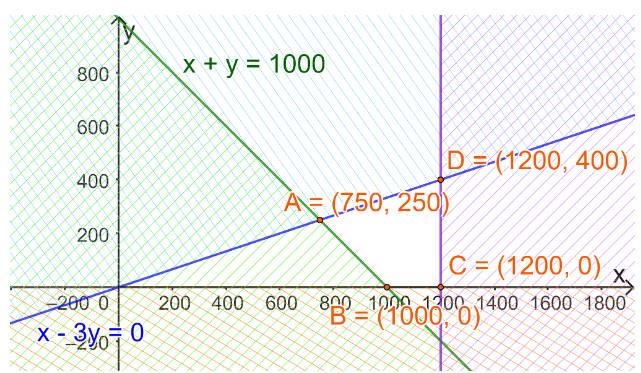
Miền nghiệm là miền tứ giác ABCD với: A(750;250); B(1000;0); C(1200;0); D(1200;400)
Lợi nhuận thu được sau một năm là
\(\begin{array}{*{20}{l}}{F\left( {x;y} \right) = x.7\% \; + y.8\% \; + (1200 - x - y).12\% }\\{ = 144 - 0,05x - 0,04y}\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Thay tọa độ các điểm A, B vào biểu thức F(x;y) ta được:
\(F\left( {750;250} \right) = 144 - 0,05.750 - 0,04.250 = 96,5\)
\(F\left( {1000;0} \right) = 144 - 0,05.1000 - 0,04.0 = 94\)
\(F\left( {1200;0} \right) = 144 - 0,05.1200 - 0,04.0 = 84\)
\(F\left( {1200;400} \right) = 144 - 0,05.1200 - 0,04.400 = 68\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=750 và y=250.
Vậy bác An nên đầu tư 750 trái phiếu chính phủ; 250 triệu đồng trái phiếu ngân hàng và 200 triệu trái phiếu doanh nghiệp.
Tham khảo:
Cách 2:
Bước 1: 1,2 tỉ đồng=1200 (triệu đồng)
Gọi x là số tiền mua trái phiếu ngân hàng và y là số tiền mua trái phiếu doanh nghiệp.
Khi đó \(x \ge 0,y \ge 0\).
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ nên số tiền đầu tư trái phiếu chính phủ là \(1200 - x - y\) (triệu đồng)
Số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có: \(1200 - x - y \ge 3x \Leftrightarrow 4x + y \le 1200\)
Bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(y \le 200\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Xác định miền nghiệm là miền tứ giác OABC với:
O(0;0); A(300;0); B(250;200); C(0;200).
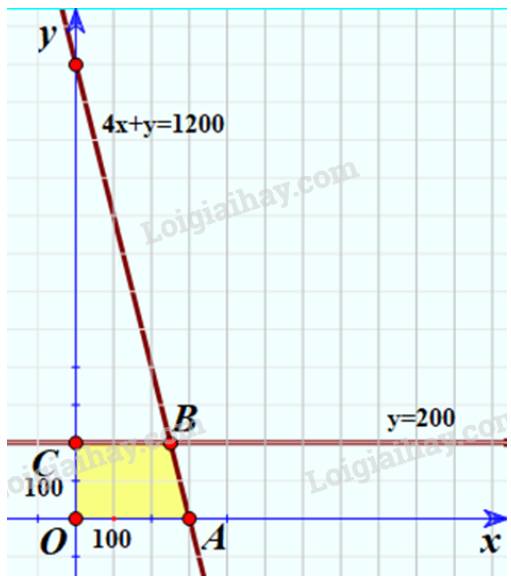
Bước 2: Lợi nhuận thu được sau một năm là
\(\begin{array}{l}F\left( {x;y} \right) = \left( {1200 - x - y} \right).7\% + x.8\% + y.12\% \\ = 84 + 0,01x + 0,05y\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Thay tọa độ các điểm O, A, B, C vào biểu thức F(x;y) ta được:
\(F\left( {0;0} \right) = 80\)
\(F\left( {300;0} \right) = 84 + 0,01.300 + 0,05.0 = 87\)
\(F\left( {250;200} \right) = 84 + 0,01.250 + 0,05.200 = 96,5\)
\(F\left( {0;200} \right) = 84 + 0,01.0 + 0,05.200 = 94\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=250 và y=200.
Vậy bác An nên đầu tư 250 triệu đồng trái phiếu ngân hàng, 200 triệu trái phiếu doanh nghiệp và 750 trái phiếu chính phủ.

a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)
\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)
\(=14\)
a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1

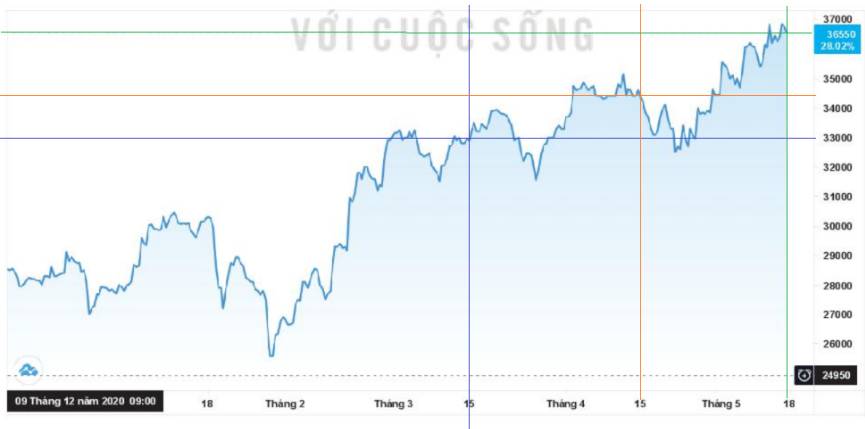
Số cổ phiếu mà anh Tiến mua được là: \(898\;200\;000:24\;950 = 36\;000\) (cổ phiếu)
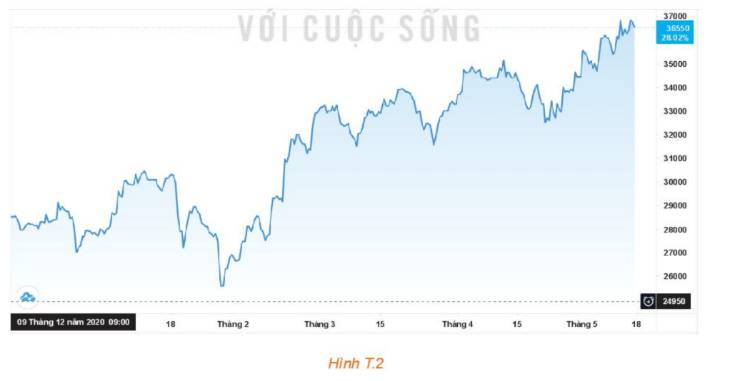
a) Vào thời điểm 15-3-2021, giá mỗi cổ phiếu là 33 000 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;33\;000 = 1\;188\;000\;000\)(đồng)
b) Vào thời điểm 15-4-2021, giá mỗi cổ phiếu là 34 400 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;34\;400 = 1\;238\;400\;000\)(đồng)
c) Vào thời điểm 18-5-2021, giá mỗi cổ phiếu là 36 550 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;36\;550 = 1\;315\;800\;000\)(đồng)

a) Tổng số tiền mẹ Việt rút ra được là:
\(T = 2\;000\;000\;000.{(1 + 7\% )^3} = 2\;450\;086\;000\)(đồng)
b) Với số tiền nêu trên, mẹ Việt mua được căn hộ chung cư với diện tích là:
\(2\;450\;086\;000:30\;626\;075 = 80\)(mét vuông)
TRAO ĐỔI
Để mua được căn hộ 100 mét vuông, cần số tiền là:
\(30\;626\;075.100 = 3\;062\;607\;500\)(đồng)
Gọi A là số tiền gửi vào (đơn vị đồng).
Ở thời điểm tháng 1 năm 2021, số tiền thu được là:
\(\begin{array}{l}T = A.{(1 + 7\% )^3} = 3\;062\;607\;500\\ \Rightarrow A = 3\;062\;607\;500:{(1 + 7\% )^3} = 2\;500\;000\;000\end{array}\)
Vậy để mua được căn hộ 100 mét vuông ở thời điểm tháng 1 năm 2021, mẹ Việt cần phải gửi tiết kiệm từ tháng 1 năm 2018 số tiền là 2 500 000 000 đồng.