Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số tiền cô Lan thu được nếu bán vào thời điểm 27-7-2020 là:
\(86\;000\;.\;5\;000 = 430\;000\;000\)(đồng)
Số tiền cô Lan thu được nếu bán vào thời điểm 30-12-2020 là:
\(108\;800\;.\;5\;000 = 544\;000\;000\)(đồng)
Số tiền cô Lan thu được nếu bán vào thời điểm 10-5-2021 là:
\(91\;000\;.\;5\;000 = 455\;000\;000\)(đồng)
b) Lãi suất 6%/năm cho kì hạn một tháng, tương ứng là 6:12=0,5(%)/ tháng
Vậy số tiền cô Lan nhận được sau 11 tháng là:
\(T = 511\;000\;000.{(1 + 0,5\% )^{11}} \approx 539\;818\;271\)(đồng)
TRAO ĐỔI
a) Với tình huống như trên cô Lan nên đầu tư ở thời điểm 27-7-2020 và bán ra vào thời điểm 30-12-2020.
b)
+) Nếu cô Lan gửi tiết kiệm, đến ngày 10-5-2021, số tiền thu được là: \(539\;818\;271\)(đồng)
+) Nếu cô Lan đầu tư, thì đến ngày 10-5-2021, số tiền thu được là: \(455\;000\;000\)(đồng)
=> Như vậy cô Lan nên chọn hình thức tiết kiệm.

Cách 1:
Gọi x là số tiền mua trái phiếu chính phủ và y là số tiền mua trái phiếu ngân hàng. (đơn vị triệu đồng) (\(x,y \le 1200\))
Khi đó, số tiền mua trái phiếu doanh nghiệp là \(1200 - x - y\)(triệu đồng)
Vì số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên \(x \ge 3y\)
Vì bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(1200 - x - y \le 200 \Leftrightarrow x + y \ge 1000\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Biểu diễn miền nghiệm của hệ trong mp tọa độ ta được
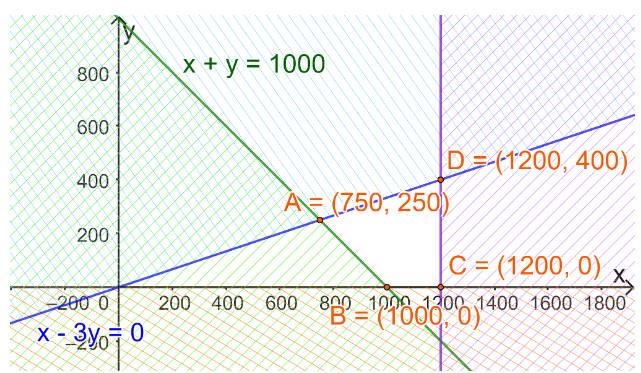
Miền nghiệm là miền tứ giác ABCD với: A(750;250); B(1000;0); C(1200;0); D(1200;400)
Lợi nhuận thu được sau một năm là
\(\begin{array}{*{20}{l}}{F\left( {x;y} \right) = x.7\% \; + y.8\% \; + (1200 - x - y).12\% }\\{ = 144 - 0,05x - 0,04y}\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Thay tọa độ các điểm A, B vào biểu thức F(x;y) ta được:
\(F\left( {750;250} \right) = 144 - 0,05.750 - 0,04.250 = 96,5\)
\(F\left( {1000;0} \right) = 144 - 0,05.1000 - 0,04.0 = 94\)
\(F\left( {1200;0} \right) = 144 - 0,05.1200 - 0,04.0 = 84\)
\(F\left( {1200;400} \right) = 144 - 0,05.1200 - 0,04.400 = 68\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=750 và y=250.
Vậy bác An nên đầu tư 750 trái phiếu chính phủ; 250 triệu đồng trái phiếu ngân hàng và 200 triệu trái phiếu doanh nghiệp.
Tham khảo:
Cách 2:
Bước 1: 1,2 tỉ đồng=1200 (triệu đồng)
Gọi x là số tiền mua trái phiếu ngân hàng và y là số tiền mua trái phiếu doanh nghiệp.
Khi đó \(x \ge 0,y \ge 0\).
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ nên số tiền đầu tư trái phiếu chính phủ là \(1200 - x - y\) (triệu đồng)
Số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có: \(1200 - x - y \ge 3x \Leftrightarrow 4x + y \le 1200\)
Bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(y \le 200\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Xác định miền nghiệm là miền tứ giác OABC với:
O(0;0); A(300;0); B(250;200); C(0;200).
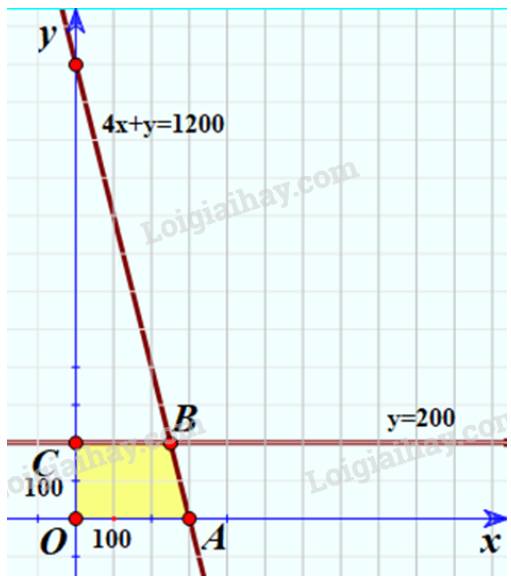
Bước 2: Lợi nhuận thu được sau một năm là
\(\begin{array}{l}F\left( {x;y} \right) = \left( {1200 - x - y} \right).7\% + x.8\% + y.12\% \\ = 84 + 0,01x + 0,05y\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Thay tọa độ các điểm O, A, B, C vào biểu thức F(x;y) ta được:
\(F\left( {0;0} \right) = 80\)
\(F\left( {300;0} \right) = 84 + 0,01.300 + 0,05.0 = 87\)
\(F\left( {250;200} \right) = 84 + 0,01.250 + 0,05.200 = 96,5\)
\(F\left( {0;200} \right) = 84 + 0,01.0 + 0,05.200 = 94\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=250 và y=200.
Vậy bác An nên đầu tư 250 triệu đồng trái phiếu ngân hàng, 200 triệu trái phiếu doanh nghiệp và 750 trái phiếu chính phủ.

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 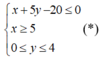
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
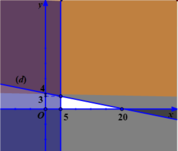
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)
\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)
\(=14\)
a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1

Giải:
Gọi số tiền ông Sáu gửi ban đầu là x.
Theo đề bài ta có:
Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)
Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)
Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)
Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)
Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng
Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.
Tổng % lãi suất trong 2 năm là :
6% . 2 = 12%
Số tiền lãi trong 2 năm là :
112360000 . 12% = 13483200
=> Tiền ông Sáu gửi là :
112360000 - 13483200 = 98876800

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.
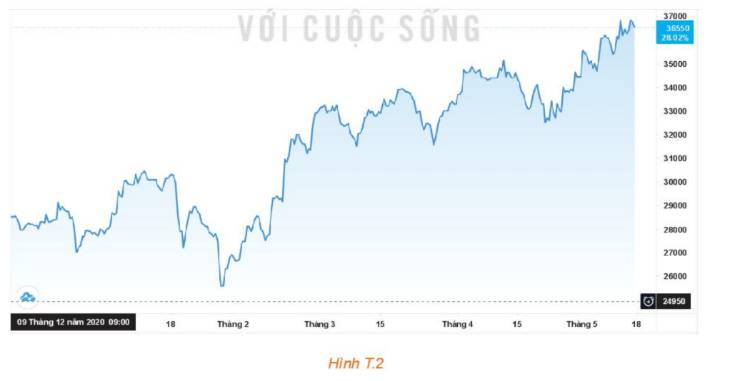

Số cổ phiếu mà anh Tiến mua được là: \(898\;200\;000:24\;950 = 36\;000\) (cổ phiếu)
a) Vào thời điểm 15-3-2021, giá mỗi cổ phiếu là 33 000 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;33\;000 = 1\;188\;000\;000\)(đồng)
b) Vào thời điểm 15-4-2021, giá mỗi cổ phiếu là 34 400 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;34\;400 = 1\;238\;400\;000\)(đồng)
c) Vào thời điểm 18-5-2021, giá mỗi cổ phiếu là 36 550 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;36\;550 = 1\;315\;800\;000\)(đồng)