
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Công thức đây nhé (Áp dụng làm thử đi)
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc , kí hiệu .Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc , kí hiệu .
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu .
Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của góc , kí hiệu .

Câu 15:
Gọi $x_0$ là nghiệm chung của 2 pt thì:
\(\left\{\begin{matrix}
x_0^2+ax_0+1=0\\
x_0^2-x_0-a=0\end{matrix}\right.\Rightarrow x_0(a+1)+(a+1)=0\)
\(\Leftrightarrow (x_0+1)(a+1)=0\)
Hiển nhiên $a\neq -1$ để 2 PT không trùng nhau. Do đó $x_0=-1$ là nghiệm chung của 2 PT
Thay vào:
$(-1)^2+a(-1)+1=0$
$\Leftrightarrow 1-a+1=0\Rightarrow a=2$
Đáp án C.
Câu 16:
D sai. Trong tam giác vuông tại $A$ là $ABC$, $\cos (90^0-\widehat{B})=\cos \widehat{C}$ và không có cơ sở để khẳng định $\cos \widehat{C}=\sin \widehat{C}$


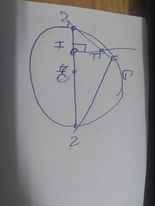
Xét (O) có
ΔMEN nội tiếp
MN là đường kính
Do đó: ΔMEN vuông tại E
=>\(\widehat{MEN}=90^0\)
=>\(\widehat{FEN}=90^0\)
Xét tứ giác HFEN có
\(\widehat{FHN}+\widehat{FEN}=90^0+90^0=180^0\)
=>HFEN là tứ giác nội tiếp
=>H,F,E,N cùng thuộc một đường tròn

Câu 1:
1: Ta có: \(A=3\sqrt{25}-\sqrt{36}-\sqrt{64}\)
\(=3\cdot5-6-8\)
\(=15-6-8=1\)
Câu I:
2: Ta có: \(B=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{x+1}{x-1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{x+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-\sqrt{x}+x+\sqrt{x}-x-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1}{x-1}=1\)

Với \(n>0;n\in N:\dfrac{1}{n\sqrt{n+4}+\left(n+4\right)\sqrt{n}}=\dfrac{1}{\sqrt{n\left(n+4\right)}\left(\sqrt{n}+\sqrt{n+4}\right)}=\dfrac{\sqrt{n+4}-\sqrt{n}}{\sqrt{n\left(n+4\right)}\left(n+4-n\right)}=\dfrac{1}{4}\left(\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+4}}\right)\) (1)
Áp dụng (1) ta được:
\(\dfrac{1}{1\sqrt{5}+5\sqrt{1}}+\dfrac{1}{5\sqrt{9}+9\sqrt{5}}+...+\dfrac{1}{2013\sqrt{2017}+2017\sqrt{2013}}\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{5}}-\dfrac{1}{\sqrt{9}}+...+\dfrac{1}{\sqrt{2013}}-\dfrac{1}{\sqrt{2017}}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{\sqrt{2017}}\right)=\dfrac{\sqrt{2017}-1}{4\sqrt{2017}}=\dfrac{2017-\sqrt{2017}}{8068}\)
Ý A

\(\dfrac{1}{2x_1+x_2-\dfrac{1}{3}}+\dfrac{1}{x_1+2x_2-\dfrac{1}{3}}\)
\(=\dfrac{x_1+2x_2-\dfrac{1}{2}+2x_1+x_2-\dfrac{1}{3}}{\left(2x_1+x_2-\dfrac{1}{3}\right)\left(x_1+2x_2-\dfrac{1}{3}\right)}\)
\(=\dfrac{3x_1+3x_2-\dfrac{2}{3}}{2x_1^2+4x_1x_2-\dfrac{2}{3}x_1+x_1x_2+2x_2^2-\dfrac{1}{3}x_2-\dfrac{1}{3}x_1-\dfrac{2}{3}x_2+\dfrac{1}{9}}\)
\(=\dfrac{3x_1+3x_2-\dfrac{2}{3}}{2x_1^2+5x_1x_2-x_1+2x_2^2-x_2+\dfrac{1}{9}}\)
\(=\dfrac{3\left(x_1+x_2-\dfrac{2}{3}\right)}{2\left(x_1^2+x_2^2\right)-\left(x_1+x_2\right)+5x_1x_2+\dfrac{1}{9}}\)
\(=\dfrac{3\left(x_1+x_2-\dfrac{2}{3}\right)}{2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-\left(x_1+x_2\right)+5x_1x_2+\dfrac{1}{9}}\)
Áp dụng định lí Vi-ét : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{4}{12}=\dfrac{1}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{3}{12}=-\dfrac{1}{4}\end{matrix}\right.\)
Ta được : \(\dfrac{3\left(\dfrac{1}{3}-\dfrac{2}{3}\right)}{2\left[\left(\dfrac{1}{3}\right)^2-2\cdot\left(-\dfrac{1}{4}\right)\right]-\dfrac{1}{3}+5\cdot\left(-\dfrac{1}{4}\right)+\dfrac{1}{9}}=4\)

3:
Tháng 4 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+100\cdot2536+1\cdot2834=628434\left(đồng\right)\)
Tháng 5 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+98\cdot2536=620528\left(đồng\right)\)
=>Giảm 1,3%






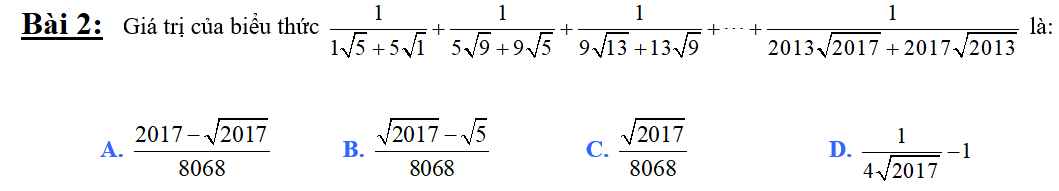

 làm giúp e câu 3, 4 với ạ
làm giúp e câu 3, 4 với ạ