K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
\(1,\\ 1,M=6+5=11\\ N=\sqrt{5}-1-\sqrt{5}=-1\\ 2,\\ a,P=1+\dfrac{x-\sqrt{x}}{\sqrt{x}-1}\left(x\ge0;x\ne1\right)\\ P=1+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=1+\sqrt{x}\\ b,P>3\Leftrightarrow1+\sqrt{x}>3\\ \Leftrightarrow\sqrt{x}>2\Leftrightarrow x>4\)
2
19 tháng 5 2022
Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
19 tháng 5 2022
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
2 tháng 9 2021
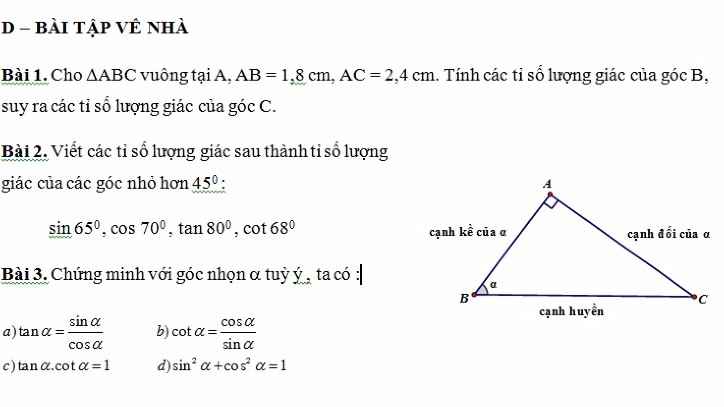
Bài 2:
\(\sin65^0=\cos25^0\)
\(\cos70^0=\sin20^0\)
\(\tan80^0=\cot10^0\)
\(\cot68^0=\tan22^0\)
NT
1
28 tháng 10 2016
\(\sqrt{51-7\sqrt{8}}=\sqrt{7^2-7.2\sqrt{2}+\left(\sqrt{2}\right)^2}=\sqrt{\left(7-\sqrt{2}\right)^2}=7-\sqrt{2}\)
(vì\(7=\sqrt{49}>\sqrt{2}\Rightarrow7-\sqrt{2}>0\))
TN
1
17 tháng 6 2023
a: Δ=(3m+1)^2-4(2m^2+m-1)
=9m^2+6m+1-8m^2-4m+4
=m^2+2m+5=(m+1)^2+4>=4
Do đó: PT luôn có hai nghiệm pb
b: A=(x1+x2)^2-5x2x1
=(3m+1)^2-5(2m^2+m-1)
=9m^2+6m+1-10m^2-5m+5
=-m^2+m+6
=-(m^2-m-6)
=-(m^2-m+1/4-25/4)
=-(m-1/2)^2+25/4<=25/4
Dấu = xảy ra khi m=1/2
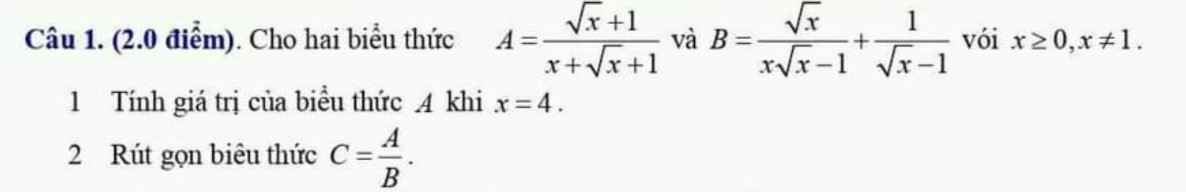
Câu 4:
1: Xét (O) có
OI là một phần đường kính
CD là dây
I là trung điểm của CD
Do đó: OI⊥CD
Xét tứ giác OIAM có
\(\widehat{OIM}=\widehat{OAM}=90^0\)
Do đó: OIAM là tứ giác nội tiếp
hay O,I,A,M cùng thuộc 1 đường tròn(1)
Xét tứ giác OIBM có
\(\widehat{OIM}+\widehat{OBM}=180^0\)
Do đó: OIBM là tứ giác nội tiếp
hay O,I,B,M cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra O,I,A,M,B cùng thuộc 1 đường tròn