
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)

3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)

\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)

4:
a: \(=5x^2y^2\cdot\dfrac{7}{10}x^4y\cdot40x^2z^3\)
\(=\left(5\cdot\dfrac{7}{10}\cdot40\right)\left(x^2y^2\cdot x^4y\cdot x^2z^3\right)\)
\(=140x^8y^3z^3\)
Bậc là 8+3+3=14
b: \(=-\dfrac{1}{2}\cdot ab\cdot\dfrac{-4}{3}\cdot a^2bc\cdot5c^2b^3\)
\(=\left(\dfrac{1}{2}\cdot\dfrac{4}{3}\cdot5\right)\cdot ab\cdot a^2b\cdot c\cdot c^2b^3\)
\(=\dfrac{10}{3}a^3b^5c^3\)
Bậc là 11
c: \(=-1.2\cdot ab\cdot100a^4b^2\cdot c^3\cdot\left(-1.5\right)\cdot a^2c\)
\(=1.8\cdot100\cdot ab\cdot a^4b^2c^3\cdot a^2c\)
\(=180a^7b^3c^4\)
Bậc là 14

Bài 8:
a) \(x^2-25x=0\)
\(\Leftrightarrow x\left(x-25\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-25=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=25\end{matrix}\right.\)
b) \(7x\left(x-3\right)-5\left(3-x\right)=0\)
\(\Leftrightarrow7x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(7x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\7x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{7}\end{matrix}\right.\)
c) \(7x\left(x+4\right)-7x-28=0\)
\(\Leftrightarrow7x\left(x+4\right)-7\left(x+4\right)=0\)
\(\Leftrightarrow7\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\)
d) \(\left(2x^2+5x\right)\left(x^2-x\right)+\left(2x^2+10\right)\left(x-x^2\right)=0\)
\(\Leftrightarrow\left(2x^2+5x\right)\left(x^2-x\right)-\left(2x^2+10\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-x\right)\left(2x^2+5x-2x^2-10\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(5x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\5x-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
7:
a: \(4a^3b-12a^2b^2+8ab^3\)
\(=4ab\cdot a^2-4ab\cdot3ab+4ab\cdot2b^2\)
\(=4ab\left(a^2-3ab+2b^2\right)\)
\(=4ab\left(a^2-ab-2ab+2b^2\right)\)
\(=4ab\left[a\left(a-b\right)-2b\left(a-b\right)\right]\)
\(=4ab\left(a-b\right)\left(a-2b\right)\)
b: \(\dfrac{5}{2}x^4+\dfrac{3}{4}x^3-\dfrac{1}{5}x^2\)
\(=x^2\cdot\dfrac{5}{2}x^2+x^2\cdot\dfrac{3}{4}x-x^2\cdot\dfrac{1}{5}\)
\(=x^2\left(\dfrac{5}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{5}\right)\)
c: \(3x^2\left(x+9\right)-2\left(x+9\right)\)
\(=\left(x+9\right)\cdot3x^2-\left(x+9\right)\cdot2\)
\(=\left(x+9\right)\left(3x^2-2\right)\)
d: \(3x^2\left(7x+y\right)-5x\left(7x+y\right)+14x+2y\)
\(=\left(7x+y\right)\left(3x^2-5x\right)+2\left(7x+y\right)\)
\(=\left(7x+y\right)\left(3x^2-5x+2\right)\)
\(=\left(7x+y\right)\left(3x^2-3x-2x+2\right)\)
\(=\left(7x+y\right)\left[3x\left(x-1\right)-2\left(x-1\right)\right]\)
\(=\left(7x+y\right)\left(x-1\right)\left(3x-2\right)\)

\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)

a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).


 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
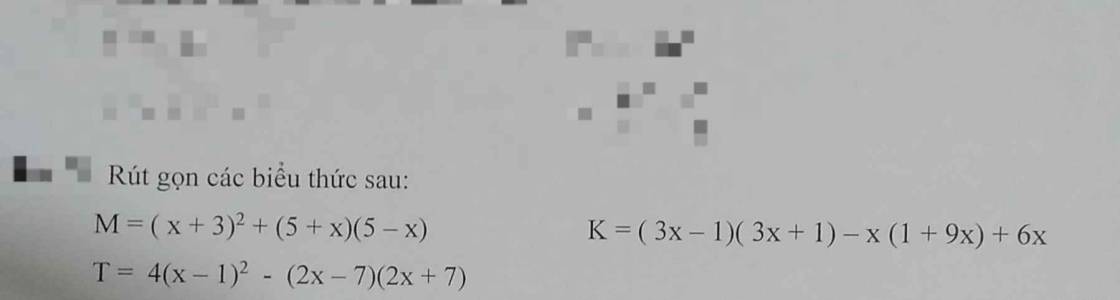
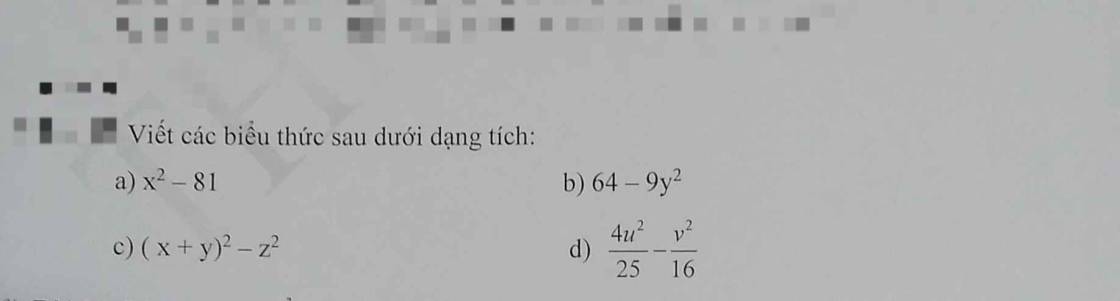


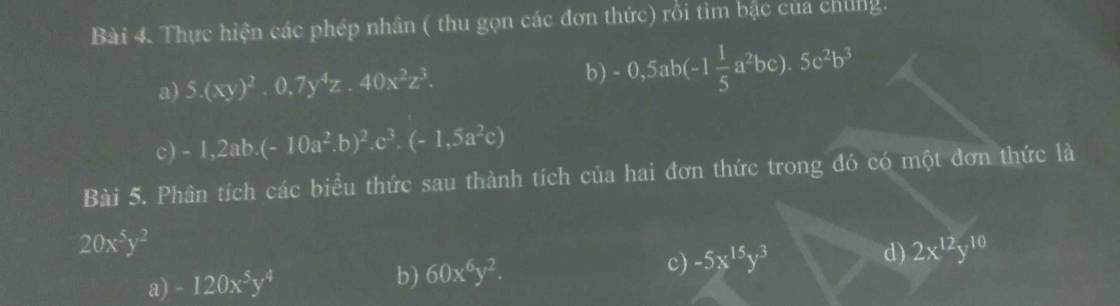

 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
Bài 12:
a) \(4x^2+4x+1=0\)
\(\Leftrightarrow\left(2x\right)^2+2\cdot2x\cdot1+1^2=0\)
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Leftrightarrow2x+1=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
b) \(x^2-2x=-1\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)
c) \(-x^2+10x=25\)
\(\Leftrightarrow-x^2+10x-25=0\)
\(\Leftrightarrow-\left(x^2-10x+25\right)=0\)
\(\Leftrightarrow-\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
d) \(9=12x-4x^2\)
\(\Leftrightarrow4x^2-12x+9=0\)
\(\Leftrightarrow\left(2x-3\right)^2=0\)
\(\Leftrightarrow2x-3=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=\dfrac{3}{2}\)