K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PD
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.1:\\ a,3x-9y=3\left(x-3y\right)\\ b,x^2-5x=x\left(x-5\right)\\ c,\left(x-3\right)\left(x-5\right)-\left(2x+1\right)\left(3-x\right)=\left(x-3\right)\left(x-5\right)+\left(x-3\right)\left(2x+1\right)\\ =\left(x-3\right)\left(x-5+2x+1\right)=\left(x-3\right)\left(3x-4\right)\\ d,3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\\ e,3\left(x+5\right)-x^2-5x=3\left(x+5\right)-x\left(x+5\right)\\ =\left(x+5\right)\left(3-x\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.2:\\ a,x^3-9x=0\\ \Leftrightarrow x.\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\\ b,5x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-2\end{matrix}\right.\\ c,x^2-7x=0\\ \Leftrightarrow x\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
20 tháng 4 2021
Bài 1:
b) Ta có: \(\dfrac{x-12}{77}+\dfrac{x-11}{78}=\dfrac{x-74}{15}+\dfrac{x-73}{16}\)
\(\Leftrightarrow\dfrac{x-12}{77}-1+\dfrac{x-11}{78}-1=\dfrac{x-74}{15}-1+\dfrac{x-73}{16}-1\)
\(\Leftrightarrow\dfrac{x-89}{77}+\dfrac{x-89}{78}-\dfrac{x-89}{15}-\dfrac{x-89}{16}=0\)
\(\Leftrightarrow\left(x-89\right)\left(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
mà \(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\ne0\)
nên x-89=0
hay x=89
Vậy: S={89}
20 tháng 4 2021
Bài 1:
a)ĐKXĐ: \(x\notin\left\{3;-1\right\}\)
Ta có: \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2x+2}=\dfrac{2x}{\left(x-3\right)\left(x+1\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x-3\right)\left(x+1\right)}\)
Suy ra: \(x^2+x+x^2-3x-4x=0\)
\(\Leftrightarrow x^2-6x=0\)
\(\Leftrightarrow x\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhân\right)\\x=6\left(nhận\right)\end{matrix}\right.\)
Vậy: S={0;6}
6 tháng 3 2021
Bài 5:
a) Ta có: \(P=\left(\dfrac{1}{x-1}-\dfrac{1}{x}\right):\left(\dfrac{x+1}{x-2}-\dfrac{x+2}{x-1}\right)\)
\(=\left(\dfrac{x}{x\left(x-1\right)}-\dfrac{x-1}{x\left(x-1\right)}\right):\left(\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-2\right)\left(x-1\right)}-\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-1\right)}\right)\)
\(=\dfrac{x-x+1}{x\left(x-1\right)}:\dfrac{x^2-1-\left(x^2-4\right)}{\left(x-2\right)\left(x-1\right)}\)
\(=\dfrac{1}{x\left(x-1\right)}:\dfrac{x^2-1-x^2+4}{\left(x-2\right)\left(x-1\right)}\)
\(=\dfrac{1}{x\left(x-1\right)}\cdot\dfrac{\left(x-2\right)\left(x-1\right)}{3}\)
\(=\dfrac{x-2}{3x}\)
CH
3
6 tháng 12 2017
Ta có:\(x^3-7x-6=\left(x^3-3x^2\right)+\left(3x^2-9x\right)+\left(2x-6\right)\)
\(=\left(x-3\right)\left(x^2+3x+2\right)=\left(x-3\right)\left(x^2+2x+x+2\right)\)
\(=\left(x-3\right)\left(x+2\right)\left(x+1\right)\)
BT
6 tháng 12 2017
=x3-x-6x-6
=(x3-x)-(6x-6)
=x(x2-1)-6(x-1)
=x(x-1)(x+1)-6(x-1)
=(x-1)(x2+1-6)
H9
HT.Phong (9A5)
CTVHS
18 tháng 11 2023
Bài 8:
a) \(x^2-25x=0\)
\(\Leftrightarrow x\left(x-25\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-25=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=25\end{matrix}\right.\)
b) \(7x\left(x-3\right)-5\left(3-x\right)=0\)
\(\Leftrightarrow7x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(7x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\7x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{7}\end{matrix}\right.\)
c) \(7x\left(x+4\right)-7x-28=0\)
\(\Leftrightarrow7x\left(x+4\right)-7\left(x+4\right)=0\)
\(\Leftrightarrow7\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\)
d) \(\left(2x^2+5x\right)\left(x^2-x\right)+\left(2x^2+10\right)\left(x-x^2\right)=0\)
\(\Leftrightarrow\left(2x^2+5x\right)\left(x^2-x\right)-\left(2x^2+10\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-x\right)\left(2x^2+5x-2x^2-10\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(5x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\5x-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
18 tháng 11 2023
7:
a: \(4a^3b-12a^2b^2+8ab^3\)
\(=4ab\cdot a^2-4ab\cdot3ab+4ab\cdot2b^2\)
\(=4ab\left(a^2-3ab+2b^2\right)\)
\(=4ab\left(a^2-ab-2ab+2b^2\right)\)
\(=4ab\left[a\left(a-b\right)-2b\left(a-b\right)\right]\)
\(=4ab\left(a-b\right)\left(a-2b\right)\)
b: \(\dfrac{5}{2}x^4+\dfrac{3}{4}x^3-\dfrac{1}{5}x^2\)
\(=x^2\cdot\dfrac{5}{2}x^2+x^2\cdot\dfrac{3}{4}x-x^2\cdot\dfrac{1}{5}\)
\(=x^2\left(\dfrac{5}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{5}\right)\)
c: \(3x^2\left(x+9\right)-2\left(x+9\right)\)
\(=\left(x+9\right)\cdot3x^2-\left(x+9\right)\cdot2\)
\(=\left(x+9\right)\left(3x^2-2\right)\)
d: \(3x^2\left(7x+y\right)-5x\left(7x+y\right)+14x+2y\)
\(=\left(7x+y\right)\left(3x^2-5x\right)+2\left(7x+y\right)\)
\(=\left(7x+y\right)\left(3x^2-5x+2\right)\)
\(=\left(7x+y\right)\left(3x^2-3x-2x+2\right)\)
\(=\left(7x+y\right)\left[3x\left(x-1\right)-2\left(x-1\right)\right]\)
\(=\left(7x+y\right)\left(x-1\right)\left(3x-2\right)\)
LP
mn giúp mik vs ạ bài nào cx đc ạ cả 2 thì càng tốt mik cảm ơn vì bài hơi dài nên mon mn thông cảm :)
1
8 tháng 9 2021
Câu 106:
a: Xét ΔABC có
P là trung điểm của AB
N là trung điểm của AC
Do đó: PN là đường trung bình của ΔABC
Suy ra: PN//BC
hay PN//HM; QN//HM
Xét tứ giác QNMH có QN//HM
nên QNMH là hình thang
mà \(\widehat{QHM}=90^0\)
nên QNMH là hình thang vuông
b: Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến ứng với cạnh huyền AC
nên \(HN=\dfrac{AC}{2}\left(1\right)\)
Xét ΔABC có
M là trung điểm của BC
P là trung điểm của AB
Do đó: MP là đường trung bình của ΔABC
Suy ra: MP//AC và \(MP=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MP=HN
Xét tứ giác MNPH có PN//HM
nên MNPH là hình thang
mà MP=HN
nên MNPH là hình thang cân
8 tháng 9 2021
bạn đinhr thực sự hâm mộ bạn luôn á cam rơn nhìu nha mong bn sẽ luôn giúp đỡ mik :)
19 tháng 7 2017
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a^3+3a^2b+3ab^2+b^3\right)+c^3-3abc-3a^2b-3ab^2=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\) (luôn đúng vì \(a+b+c=0\))
Vậy \(a^3+b^3+c^3=3abc\)
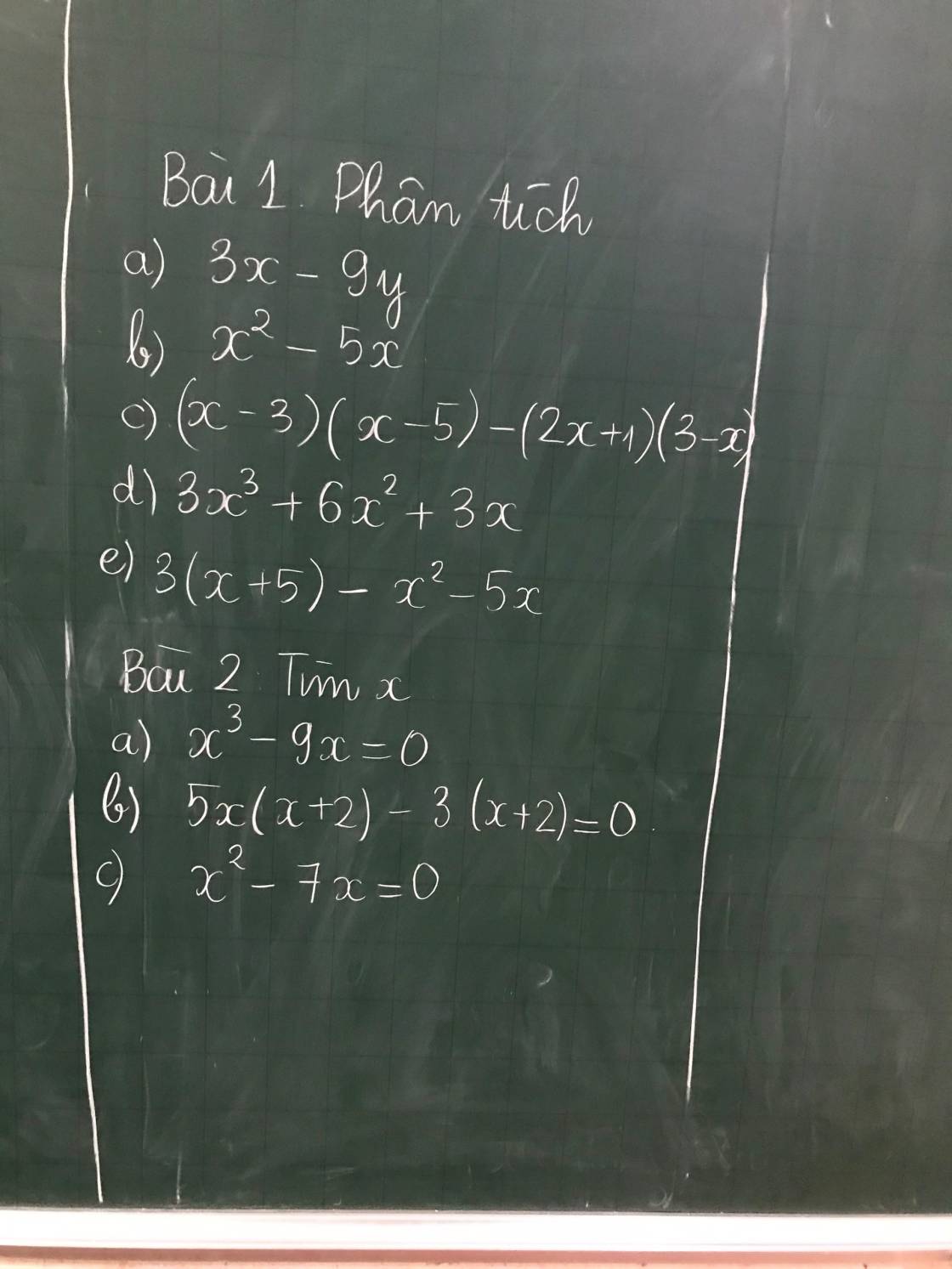
Bài 3:
a: \(x^3-x=x\left(x-1\right)\left(x+1\right)\)
b: \(x^3-4xy^2=x\left(x^2-4y^2\right)=x\left(x-2y\right)\left(x+2y\right)\)
c: \(25-4x^2=\left(5-2x\right)\left(5+2x\right)\)
d: \(x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\)
e: \(4x^2y-y=y\left(4x^2-1\right)=y\left(2x-1\right)\left(2x+1\right)\)
f: \(9-\left(x+y\right)^2=\left(3-x-y\right)\left(3+x+y\right)\)