Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x^3-x^2(m+3)+x(3m+2)-2m=0
=>(x-1)(x^2-(m+2)x+2m)=0
=>x=1 hoặc x^2-(m+2)x+2m=0
Để PT có 3 nghiệm thì (m+2)^2-4*2m>0 và 1^2-(m+2)+2m<>0
=>m<>1 và m<>2
=>x2=(m+2-m+2)/2=2 và x3=(m+2+m-2)/2=m
Để tạo thành cấp sô nhân thì
x1<x2<m hoặc m<x1<x2 hoặc x1<m<x2
=>m*1=2^2 hoặc 2m=1 hoặc m^2=2
=>m=4 hoặc m=1/2 hoặc m=căn 2

1/ \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+1\right)=f\left(2\right)=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x^2+2x+4}=\dfrac{1}{12}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=f\left(2\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
=> ham so gian doan tai x=2
2/ \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=2a-1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{3x-2-4}{\left(x-2\right)\left(\sqrt{3x-2}+2\right)}=\lim\limits_{x\rightarrow2^+}\dfrac{3}{\sqrt{3x-2}+2}=\dfrac{3}{4}\)
De ham so lien tuc tai x=2
\(\Leftrightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)\Leftrightarrow2a-1=\dfrac{3}{4}\Leftrightarrow a=\dfrac{7}{8}\)

Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 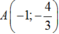 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.

Tiếp tuyến song song trục hoành \(\Rightarrow\) hệ số góc của tiếp tuyến bằng 0 \(\Rightarrow\) đó là tiếp tuyến tại các cực trị
\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-4\\x=-1\Rightarrow y=-5\\x=1\Rightarrow y=-5\end{matrix}\right.\)
Vậy các điểm đó là \(A\left(0;-4\right);B\left(-1;-5\right);C\left(-1;-5\right)\) (1 chú ý nhỏ là tiếp tuyến tại B và C trùng nhau)

Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
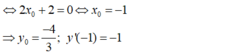
- Phương trình tiếp tuyến tại điểm 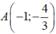 là:
là:
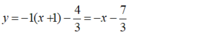
Chọn A.

- Ta có :
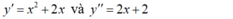
- Theo giả thiết x 0 là nghiệm của phương trình:
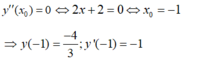
- Phương trình tiếp tuyến tại điểm 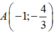 là:
là:
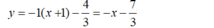
Chọn A.

1.
\(y'=12x+\dfrac{4}{x^2}\)
2.
\(y'=\dfrac{3}{\left(-x+1\right)^2}\)
3.
\(y'=\dfrac{2x-3}{2\sqrt{x^2-3x+4}}\)
4.
\(y=\dfrac{x^3+3x^2-x-3}{x-4}\)
\(y'=\dfrac{\left(3x^2+6x-1\right)\left(x-4\right)-\left(x^3+3x^2-x-3\right)}{\left(x-4\right)^2}=\dfrac{2x^3-9x^2-24x+7}{\left(x-4\right)^2}\)
5.
\(y'=-\dfrac{4x-3}{\left(2x^2-3x+5\right)^2}\)
6.
\(y'=\sqrt{x^2-1}+\dfrac{x\left(x+1\right)}{\sqrt{x^2-1}}\)




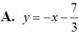
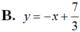
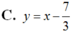
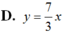
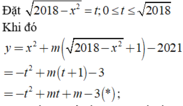


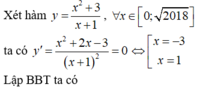
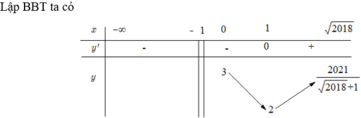
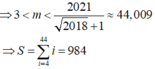
Tất cả k dưới đây là \(k\in Z\)
1.
ĐKXĐ: \(1-2cosx\ne0\Rightarrow cosx\ne\dfrac{1}{2}\)
\(\Rightarrow x\ne\pm\dfrac{\pi}{3}+k2\pi\)
2.
\(cos2x-1=0\Rightarrow cos2x=1\)
\(\Rightarrow2x=k2\pi\)
\(\Rightarrow x=k\pi\)
b.
\(\sqrt{3}cotx-3=0\Rightarrow cotx=\sqrt{3}\)
\(\Rightarrow x=\dfrac{\pi}{6}+k\pi\)
c.
\(2sin^22x+sin2x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}sin2x=-1\\sin2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{2}+k2\pi\\2x=\dfrac{\pi}{6}+k2\pi\\2x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)
3.
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:
\(\sqrt{3}^2+2^2\ge m^2\)
\(\Rightarrow m^2\le7\)
\(\Rightarrow-\sqrt{7}\le m\le\sqrt{7}\)