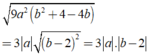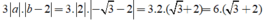K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DQ
1
7 tháng 8 2019
\(\sqrt{9a^2\left(b^2+4-4b\right)}\)
\(=\sqrt{9a^2\left(b-2\right)^2}\)
\(=\sqrt{\left[3a\left(b-2\right)\right]^2}\)
\(=\left|3a\left(b-2\right)\right|\)
+) Xét \(3a\left(b-2\right)\ge0\)
\(\Rightarrow\left|3a\left(b-2\right)\right|=3a\left(b-2\right)\)
+) Xét \(3a\left(b-2\right)< 0\)
\(\Rightarrow\left|3a\left(b-2\right)\right|=-3a\left(b-2\right)=3a\left(2-b\right)\)
Tại \(a=-2;b=-\sqrt{3}\) ta có
\(3a\left(b-2\right)=3\cdot\left(-2\right)\cdot\left(-\sqrt{3}-2\right)=12+6\sqrt{3}>0\)
Do đó : \(\left|3a\left(b-2\right)\right|=3a\left(b-2\right)=12+6\sqrt{3}\)
Vậy....
AH
Akai Haruma
Giáo viên
7 tháng 12 2019
Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(\left(\frac{4}{a}+\frac{1}{4b}\right)(a+b)\geq (2+\frac{1}{2})^2\)
\(\Leftrightarrow \left(\frac{4}{a}+\frac{1}{4b}\right).\frac{5}{4}\geq \frac{25}{4}\)
\(\Leftrightarrow \frac{4}{a}+\frac{1}{4b}\geq 5\) (đpcm)
Dấu "=" xảy ra khi \(\left\{\begin{matrix} \frac{2}{a}=\frac{1}{2b}\\ a+b=\frac{5}{4}\end{matrix}\right.\) hay $a=1; b=\frac{1}{4}$
6 tháng 10 2017
Ta có : \(a^3-a^2b+ab^2-6b^3=0\)
\(\Rightarrow a^3-2a^2b+a^2b-2ab^2+3ab^2-6b^3=0\)
\(\Rightarrow a^2\left(a-2b\right)+ab\left(a-2b\right)+3b^2\left(a-2b\right)=0\)
\(\Rightarrow\left(a-2b\right)\left(a^2+ab+3b^2\right)=0\) mà \(a>b>0\)\(\Rightarrow a^2+ab+3b^2>0\)
\(\Rightarrow a-2b=0\Rightarrow a=2b\)
thay vào B ta được : \(B=\dfrac{16b^4-4b^4}{b^4-64b^4}=-\dfrac{12b^4}{63b^4}=-\dfrac{4}{21}\)
NT
1
TS
1
