
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

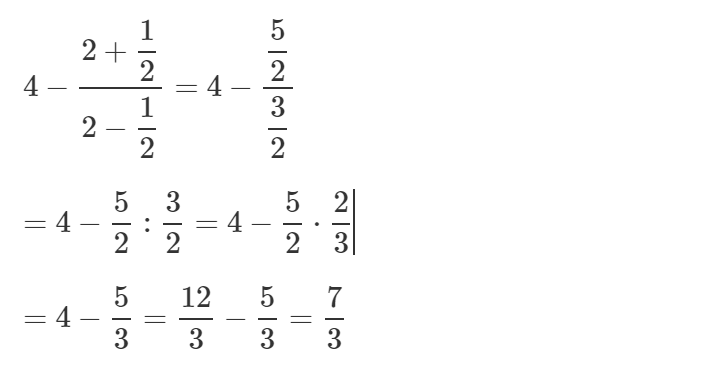


\(=\dfrac{2^4\cdot5^4\cdot3^6}{2^8\cdot3^4}=3^2\cdot5^4\cdot\dfrac{1}{2^4}\)

Ta có \(\widehat{S}+\widehat{SGQ}+\widehat{Q}=180^0\Rightarrow\widehat{S}+\widehat{Q}=180^0-\widehat{SGQ}\)
Mà \(\widehat{S}-\widehat{Q}=12^0\Rightarrow\left\{{}\begin{matrix}\widehat{S}=\dfrac{180^0-\widehat{SGQ}+12^0}{2}=96^0-\dfrac{\widehat{SGQ}}{2}\\\widehat{Q}=\dfrac{180^0-\widehat{SGQ}-12^0}{2}=84^0-\dfrac{\widehat{SGQ}}{2}\end{matrix}\right.\)
Mà GP là p/g nên \(\widehat{QGP}=\widehat{PGS}=\dfrac{\widehat{SGQ}}{2}\)
\(\Rightarrow\widehat{Q}=84^0-\widehat{QGP}\)
Ta có \(\widehat{GPS}=\widehat{Q}+\widehat{QGP}=84^0-\widehat{QGP}+\widehat{QGP}=84^0\) (tc góc ngoài)

\(\left(x-1\right)^2=\left(x-1\right)^{2018}\)
\(\Rightarrow x\in\left\{1,2\right\}\)
PP/ss: Dạ e làm đại ạ_:333
ßا§™ e làm đại hay qué :> thiếu 1 kết quả =)
\(\left(x-1\right)^2=\left(x-1\right)^{2018}\Rightarrow\left(x-1\right)^{2018}-\left(x-1\right)^2=\left(x-1\right)^2.\left[\left(x-1\right)^{2016}-1\right]=0\)
\(\Rightarrow\orbr{\begin{cases}\left(x-1\right)^2=0\\\left(x-1\right)^{2016}=1\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}\text{hoặc }x=0\)

1/4x+2/3x+4/3=0
11/12x=0-4/3
11/12x=-4/3
x=-4/3:11/12
x=-48/33

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)


\(ab=c\)
\(ac=a^2b=4b\)suy ra \(a=\pm2\)
\(a=2\Rightarrow ab=2b=c\Rightarrow bc=2b^2=18\)suy ra \(b=\pm3\)
\(b=3\) thì \(c=6\)và \(b=-3\)thì \(c=-6\)
làm tương tự với \(a=-2\)
Vậy ta có bảng
| a | b | c |
| 2 | 3 | 6 |
| 2 | -3 | -6 |
| -2 | 3 | -6 |
| -2 | -3 | 6 |

\(\left|x+\dfrac{1}{7}\right|-\dfrac{2}{3}=0\)
\(\Rightarrow\left|x+\dfrac{1}{7}\right|=0+\dfrac{2}{3}\\ \Rightarrow\left|x+\dfrac{1}{7}\right|=\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{7}=\dfrac{2}{3}\\x+\dfrac{1}{7}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-\dfrac{1}{7}\\x=-\dfrac{2}{3}-\dfrac{1}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{21}\\x=-\dfrac{17}{21}\end{matrix}\right.\)