Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c/tiếp tục áp dụng công thức bậc 2 :
(a=12;b=-25;c=12) có:
\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2.a}\)
\(\Leftrightarrow x=\dfrac{-1.-25\pm\sqrt{-25^2-4.12.12}}{2.12}\)
\(\Leftrightarrow x=\dfrac{25\pm\sqrt{49}}{24}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{25+7}{24}\\x_2=\dfrac{25-7}{24}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{4}{3}\\x_2=\dfrac{3}{4}\end{matrix}\right.\)
từ trên suy ra:
\(\dfrac{3}{4}\le x\le\dfrac{4}{3}\)
b/áp dụng công thức bậc 2 :
\(x=\dfrac{-1.-3\pm\sqrt{3^2-4.2.-2}}{2.2}\)
\(\Leftrightarrow x=\dfrac{3\pm\sqrt{25}}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{3-5}{4}\\x_2=\dfrac{3+5}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=2\end{matrix}\right.\)
Trên pc cj vẽ khó qué e tự nghiên cứu hỏi lại thầy cô nhe:<
\(\Rightarrow x\le-\dfrac{1}{2};x\ge2\)
\(\Rightarrow x\in\left\{-\infty;-\dfrac{1}{2}\right\}U\left\{\infty;2\right\}\)

a: Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{15}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{2}\)
mà AD+CD=AC=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{2}=\dfrac{AD+CD}{3+2}=\dfrac{15}{5}=3\)
=>\(AD=3\cdot3=9cm;CD=2\cdot3=6\left(cm\right)\)
b: Xét ΔABC có BD' là phân giác góc ngoài
nên \(\dfrac{D'C}{D'A}=\dfrac{BC}{BA}\)
=>\(\dfrac{D'C}{D'C+CA}=\dfrac{10}{15}=\dfrac{2}{3}\)
=>\(\dfrac{D'C}{D'C+15}=\dfrac{2}{3}\)
=>\(3D'C=2\left(D'C+15\right)\)
=>D'C=30(cm)

\(b,x^3+\left(2-x\right)^3>2x+4+6x^2\)
\(\Leftrightarrow x^3+\left(8-12x+6x^2-x^3\right)>2x+4+6x^2\)
\(\Leftrightarrow x^3+8-12x+6x^2-x^3-2x-4-6x^2>0\)
\(\Leftrightarrow-14x+4>0\)
\(\Leftrightarrow-14x>-4\)
\(\Leftrightarrow x< \dfrac{2}{7}\)
\(a,\left(1+x\right)^3-\left(x-2\right)^3>9\left(x-1\right)^2\)
\(\Leftrightarrow\left(1+3x+3x^2+x^3\right)-\left(x^3-6x^2+12x-8\right)>9\left(x^2-2x+1\right)\)
\(\Leftrightarrow1+3x+3x^2+x^3-x^3+6x^2-12x+8>9x^2-18x+9\)
\(\Leftrightarrow9x^2-9x+9>9x^2-18x+9\)
\(\Leftrightarrow9x^2-9x+9-9x^2+18x-9>0\)
\(\Leftrightarrow9x>0\)
\(\Leftrightarrow x>0\)

1) -Áp dụng đ/l phân giác ngoài của tam giác là ra, còn nếu đề bắt c/m định lí đó thì mình sẽ c/m.
-CF//AB (F thuộc AE).
-Dễ dàng c/m: \(\widehat{CAF}=\widehat{CFA}\) (cùng bằng \(\widehat{BAE}\))
\(\Rightarrow\)△ACF cân tại C \(\Rightarrow AC=CF\).
-△CEF có: AB//CF \(\Rightarrow\dfrac{BE}{CE}=\dfrac{AB}{CF}=\dfrac{AB}{AC}\)
2) -Ta có: \(\widehat{BAC}\) và \(\widehat{BAx}\) (tia Ax là tia đối của tia AB) là 2 góc kề bù.
\(\Rightarrow\widehat{DAE}=90^0\) (định lí về góc tạo bởi 2 tia p/g của 2 góc kề bù).
\(\Rightarrow\)△ADE vuông tại A.
3) -Giả sử AB>AC.
-△ABC có: AD, AE là p/g trong và ngoài.
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{BE}{CE}=\dfrac{AB}{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}\Rightarrow BD=\dfrac{AB.BC}{AB+AC}\\\dfrac{BE}{AB}=\dfrac{CE}{AC}=\dfrac{BE-CE}{AB-AC}=\dfrac{BC}{AB-AC}\Rightarrow BE=\dfrac{AB.BC}{AB-AC}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{BD}+\dfrac{1}{BE}=\dfrac{AB+AC}{AB.BC}+\dfrac{AB-AC}{AB.BC}=\dfrac{2AB}{AB.BC}=\dfrac{2}{BC}\)




a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)

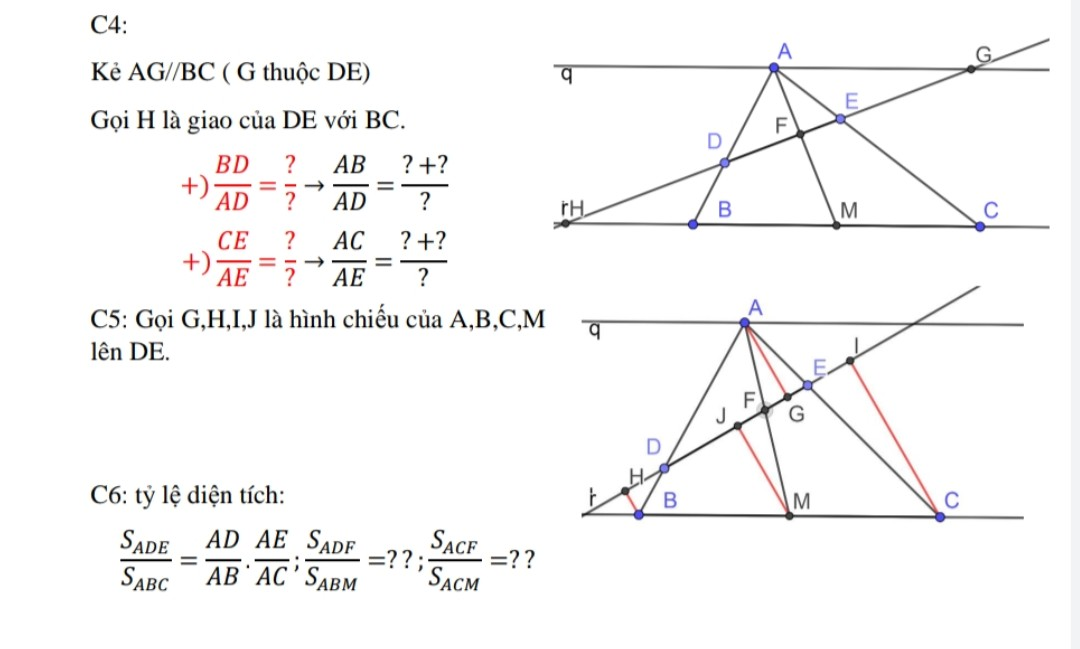 huhu giúp e với ạ
huhu giúp e với ạ