Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn cho đề thiếu thì phải vì nếu 2 góc BAC và ACD kề bù thì AB không song song với CD
Bạn xem lại đề đi

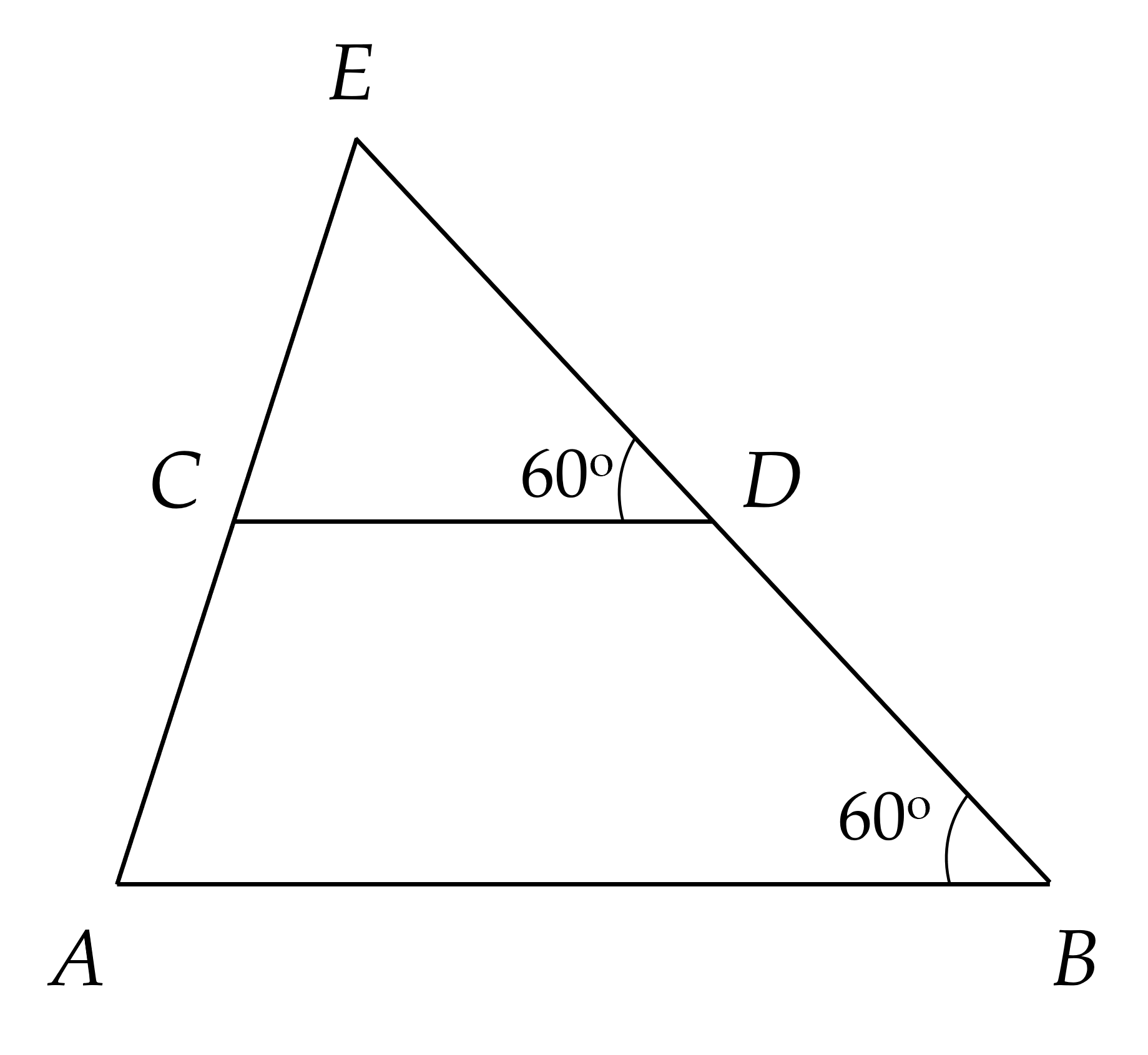
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
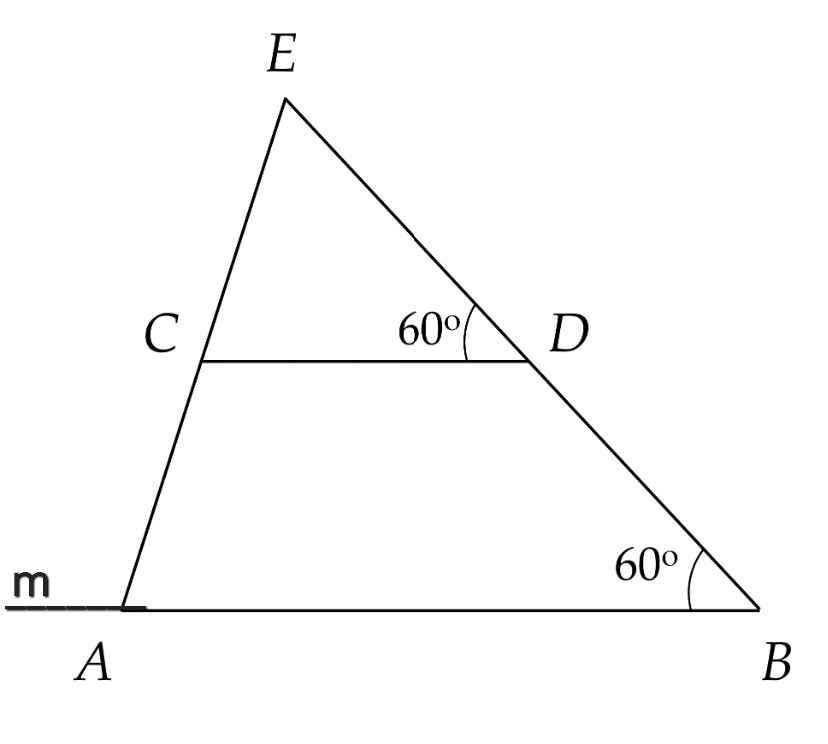
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

phần còn lại thì chứng minh CH với DE song song nhau theo giả thiết

BAD + ADC = 1800
mà 2 góc này ở vị trí trong cùng phía
=> AB // CD
mà AB _I_ BC
=> CD _I_ BC
AB // CD
=> BAC = ACD (2 góc so le trong)
mà ACD = 400
=> BAC = 400
BAD + ADC = 1800
1200 + ADC = 1800
ADC = 1800 - 1200
ADC = 600
cho mik hỏi câu b ở đâu
hôm sau yêu cầu giải có tâm tí viết a b c đi chứ thé này khó nhìn lắm

Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AEB và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {ABE} = \widehat {DCE}\)
Xét 2 tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {BDC} (= {90^o}\))
\(AB=DC\) (gt)
\(\widehat {ABE} = \widehat {DCE}\) (cmt)
=>\(\Delta AEB = \Delta DEC\)(g.c.g)