
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ đường cao AH cho tam giác ABC
sinB = AH/AB => \(\dfrac{\sqrt{3}}{2}=\dfrac{AH}{6}\Rightarrow AH=3\sqrt{3}\)cm
cosB = BH/AB => \(\dfrac{1}{2}=\dfrac{BH}{6}\Rightarrow BH=3cm\)
=> CH = BC - BH = 1 cm
Theo Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=2\sqrt{7}cm\)
-> chọn A

1: Xét ΔABC cân tại C có CI là đường trung tuyến ứng với cạnh đáy AB
nên CI là đường cao ứng với cạnh AB
Xét ΔABC cân tại B có BK là đường trung tuyến ứng với cạnh đáy AC
nên BK là đường cao ứng với cạnh AC
2: Xét ΔOBI và ΔOCK có
OB=OC
\(\widehat{IBO}=\widehat{KCO}\left(=60^0\right)\)
IB=KC
Do đó: ΔOBI=ΔOCK
Suy ra: OI=OK

Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)


a: Thay x=2 và y=-6 vào (P), ta được:
\(4\left(m+1\right)^2=-6\)(vô lý)
b: \(\left\{{}\begin{matrix}x+3y=5\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=3-4=-1\end{matrix}\right.\)
Thay x=-1 và y=2 vào (P), ta được:
\(\left(m+1\right)^2=2\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{2}-1\\m=-\sqrt{2}-1\end{matrix}\right.\)
a, hs trên đi qua B(2;-6)
<=> 4(m+1) = -6 <=> m + 1 = -3/2 <=> m = -5/2
b, Do ( x0;y0) là nghiệm hpt nên nên thay vào ta được
\(\left\{{}\begin{matrix}x_0+3y_0=5\\x_0+2y_0=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_0=2\\x_0=-1\end{matrix}\right.\)
Do hs f(x) đi qua điểm (-1;2)
<=> m + 1 = 2 <=> m = 1

Câu thứ 2 không thấy yêu cầu làm gì cả?
Câu thứ nhất:
\(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}>\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< \dfrac{a+a}{a+b+c}+\dfrac{b+b}{a+b+c}+\dfrac{c+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow1< \dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< 2\)

2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)

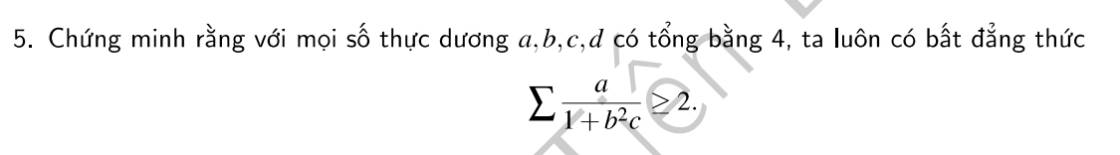
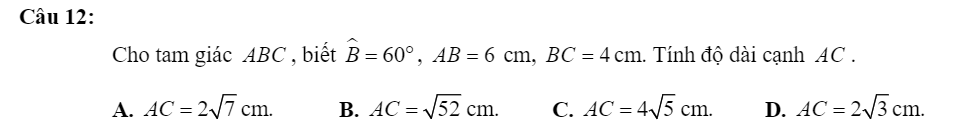



 Help mik với
Help mik với

\(a+b+c+d=4;a,b,c,d>0\)
Ta có:\(\sum\dfrac{a}{1+b^2c}=\sum\dfrac{a^2}{a+ab^2c}\ge\dfrac{\left(a+b+c+d\right)^2}{a+b+c+d+\sum ab^2c}=\dfrac{16}{4+\sum ab^2c}\)
Cần chứng minh \(\sum ab^2c\le4\). Để chứng minh BDT trên, ta chứng minh \(\left(xy+yz+zt+tx\right)\le\dfrac{\left(x+y+z+t\right)^2}{4}\left(1\right)\).
Thật vậy, bằng phép biến đổi tương đương, ta có:
\(x^2+y^2+z^2+t^2+2\left(xy+yz+zt+tx+xz+yt\right)\ge4\left(xy+yz+zt+tx\right)\)
\(\Leftrightarrow x^2+y^2+z^2+t^2-2\left(xy+yz+zt+tx\right)+2\left(xz+yt\right)\ge0\)
\(\Leftrightarrow\left(x+z\right)^2-2\left(x+z\right)\left(y+t\right)+\left(y+t\right)^2\ge0\)
\(\Leftrightarrow\left(x+z-y-t\right)^2\ge0\) (luôn đúng)
Vậy bất đẳng thức (1) đúng. Áp dụng bất đẳng thức (1), ta có:
\(\sum ab^2c\le\dfrac{\left(ab+bc+cd+da\right)^2}{4}\le\dfrac{\left[\dfrac{\left(a+b+c+d\right)^2}{4}\right]^2}{4}=4\)
Từ đây ta có điều phải chứng minh. Dấu "=" xảy ra khi \(a=b=c=d=1\)