
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bài ra ta có : \(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\)
\(5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\)
Lại có : \(\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\) (1)
\(\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\) (2)
Từ (1) và (2) suy ra: \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
\(\Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\) và \(3x-7y+5z=-30\)
Áp dụng tính chất dáy tỉ số bằng nhau ta có :
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{-30}{15}=-2\)
\(\dfrac{3x}{63}=-2\Rightarrow3x=-126\Rightarrow x=-42\)
\(\dfrac{7y}{98}=-2\Rightarrow7y=-196\Rightarrow y=-28\)
\(\dfrac{5z}{50}=-2\Rightarrow5z=-100\Rightarrow z=-20\)
Vậy \(x,y,z\) lần lượt là \(\left(-42\right),\left(-28\right)\) và \(\left(-20\right)\)

a: \(\left(\dfrac{4}{5}\right)^{2x+7}=\dfrac{625}{256}\)
=>2x+7=-4
hay x=-11/2
b: \(\left(4x-5\right)^4=\left(4x-5\right)^2\)
\(\Leftrightarrow\left(4x-5\right)^2\cdot\left(4x-4\right)\left(4x-6\right)=0\)
hay \(x\in\left\{\dfrac{5}{4};1;\dfrac{3}{2}\right\}\)
d: \(\left(8x-1\right)^{2n+1}=5^{2n+1}\)
=>8x-1=5
hay x=3/4

\(A=1+2+2^2+2^3+...+2^{2020}\)
\(2A=2+2^2+2^3+2^4+...+2^{2021}\)
\(2A-A=\left(2+2^2+2^3+2^4+....+2^{2021}\right)-\left(1+2+2^2+2^3+...+2^{2020}\right)\)
\(A=2^{2021}-1\)

\(a,\left\{{}\begin{matrix}Az\perp Ox\\Ox\perp Oy\left(\widehat{xOy}=90^0\right)\end{matrix}\right.\Rightarrow Az//Oy\)
\(b,\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \widehat{nAx}=\dfrac{1}{2}\widehat{xAz}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \Rightarrow\widehat{xOm}=\widehat{nAx}\left(=45^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(Om//An\)

Ta có: \(\text{| x - 1,5 | + | 2,5 - x | = 0}\)
Ta lại có: \(\left|x-1,5\right|\ge0\) (1)
\(\left|2,5-x\right|\ge0\) (2)
Từ (1) và (2) \(\Rightarrow\left|x-1,5\right|+\left|2,5-x\right|=0\Leftrightarrow\left\{{}\begin{matrix}x-1,5=0\\2,5-x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1,5\\x=2,5\end{matrix}\right.\)(vô lý) Vì \(x=x;1,5\ne2,5\)
Vậy không tồn tại giá trị x thõa mãn.

Xét tam giác ABC ta có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180\sigma\)
=> \(\widehat{ACB}=70\sigma\)
=> \(\widehat{BAD}=\widehat{CAD}\)= 37,5 độ
+ \(\widehat{BAE}\)= 37,5 độ + 90 độ = 127,5 độ
=> góc AEB = 180 độ - ( 35 độ + 127,5 độ )
=> góc AEB = 17,5 độ
+tam giác DAE vuông tại A có đường trung tuyến AM
=> AM = 1/2 DE => AM = ME = MD
+ AM = ME => tam giác AME cân tại M
=> góc AEM = góc EAM = 17,5 độ
+ góc AMC = góc AEM + góc EAM ( tính chất góc ngoài )
=> góc AMC = 17,5 độ + 17,5 độ = 35 độ
+ \(\widehat{ACB}=\widehat{AMC}+\widehat{CAM}\)=> góc CAM = góc ACB - góc AMC = 35 độ
=> \(\widehat{AMC}=\widehat{CAM}\)
=> tam giác ACM cân tại C ( đpcm )
c) Tam giác ACM cân tại C => AC = CM
góc ABC = góc AMC => tam giác ABM cân tại A
=> AB = AM => AB = ME ( AM = ME )
+ Chu vi tam giác ABC = AB + AC + BC
= ME + MC + BC = BE
=> chu vi tam giác ABC bằng độ dài đoạn BE

a: Xét ΔABE và ΔABF có
BE=BF
AB chung
AE=AF
Do đó: ΔABE=ΔABF
b: Xét ΔAEF và ΔBEF có
AE=BE
EF chung
AF=BF
Do đó: ΔAEF=ΔBEF
c: Xét tứ giác AEBF có
AE=BF
BE=AF
Do đó: AEBF là hình bình hành
=>AE//BF; AF//BE
 Help Me😭😭😭
Help Me😭😭😭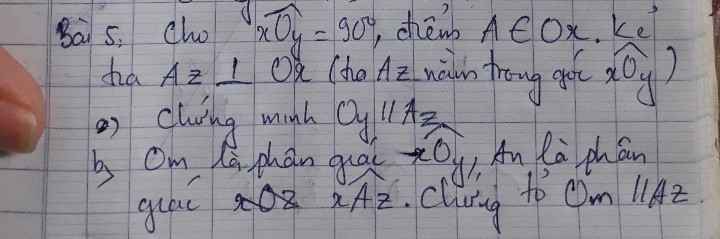
ko hieu j het tron