Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

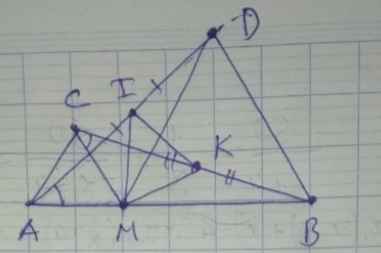
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M

khongcamxuc_123 đó nha bn bn phải giữ lời hứa đấy nha
~~~~ hok tốt ~~~~!!!!

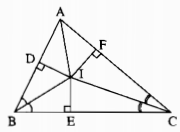
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
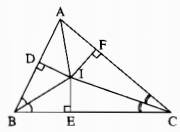
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W

Bạn tham khảo bài tương tự mà mình làm đây nhé:
Bài 1:

Bạn thay điểm E thành điểm F và điểm K thành điểm E nhé.
a)
Xét tam giác ABM và tam giác ADM có:
AB = AD (gt)
BM = DM (vì M là trung điểm của BD)
AM là cạnh chung
=> Tam giác ABM = Tam giác ADM (c . c . c)
b) Xét tam giác ABD có:
AB = AD (gt)
=> Tam giác ABD cân tại A.
Có M là trung điểm của BD
=> AM là đường trung tuyến của tam giác ABD.
=> AM đồng thời là đường trung trực của tam giác ABD.
=> AM là đường trung trực của đoạn thẳng BD.
c) Theo câu b) ta có tam giác ABM = tam giác ADM.
=> BAM = DAM (2 góc tương ứng)
Hay BAE = DAE.
Xét tam giác ABE và tam giác ADE có:
AB = AD (gt)
BAE = DAE (cmt)
AE là cạnh chung
=> Tam giác ABE = Tam giác ADE (c . g . c)
=> ABE = ADE (2 góc tương ứng).
=> BE = DE (2 cạnh tương ứng).
Ta có:
ABE + EBF = 1800 (vì 2 góc kề bù)
ADE + EDC = 1800 (vì 2 góc kề bù)
Mà ABE = ADE (cmt)
=> EBF = EDC.
Xét tam giác EBF và tam giác EDC có:
EB = ED (cmt)
EBF = EDC (cmt)
BF = DC (gt)
=> Tam giác EBF = Tam giác EDC (c . g . c)
=> BEF = DEC (2 góc tương ứng)
Lại có: BED + DEC = 180 (2 góc kề bù)
Mà BEF = DEC (cmt).
=> BED + BEF = 1800
Mà BED + BEF = FED.
=> FED = 1800
=> E, F, D thẳng hàng (đpcm).
Chúc bạn học tốt!

Đầu bài sai a, BH // CK
a, Ta có : \(BH\perp AM\)
\(CK\perp AM\)
\(\Rightarrow BH\)// \(CK\)
b, Xét \(\Delta vgBHM-\Delta vgCKM\)
\(BM=MC\)
\(\widehat{M_1}=\widehat{M_2}\)
\(\Rightarrow\Delta vgBHM=\Delta vgCKM\)
\(\Rightarrow HM=MK\)
Hay M là trung điểm của HK .
a) Mk nghĩ nên sửa thành chứng minh: BH song song với CK
Vì BH, CK cùng vuông góc với AM nên BH song song với CK.
b) Xét tam giác BHM và tam giác CKM có:
H = K = 90 độ ; BM=CM (gt) ; HMB = KMC (đối đỉnh)
Suy ra tam giác BHM = tam giác CKM. Suy ra HM = KM (2 cạnh tương ứng)
Hay M là TĐ của HK.
c) Nên sửa thành cm MH song song với BK
Xét tam giác BMK và tam giác CMH có:
BM = CM (gt) ; BMK = CMH (đối đỉnh) ; MK = MH (theo câu b)
Suy ra tam giác BMK = tam giác CMH (c.g.c) Suy ra KBM = HCM ( 2 góc tương ứng)
Mà hai góc này lại ở vị trí so le trong nên MH song song với BK