Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

=1(1+1) + 2(2+1) + 3(3+1) +...+n(n+1)
=(1^2 + 2^2 + 3^2 +...+ n^2) + (1 + 2 + 3 + ...+ n)
ta có các công thức:
1^2 + 2^2 + 3^2 +...+ n^2 = n(n+1)(2n+1)/6
1 + 2 + 3 + ...+ n = n(n+1)/2
thay vào ta có:
S = n(n+1)(2n+1)/6 + n(n+1)/2
=n(n+1)/2[(2n+1)/3 + 1]
=n(n+1)(n+2)/3

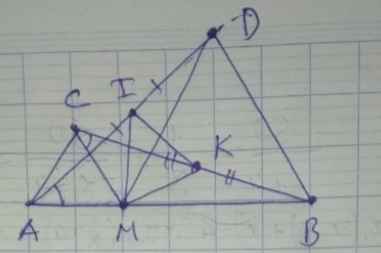
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M

a) Xét tam giác ABI và tam giác AMI:
AI chung.
AB = AM (gt).
\(\widehat{BAI}=\widehat{MAI}\) (AI là phân giác \(\widehat{BAC}\)).
\(\Rightarrow\Delta ABI=\Delta AMI\left(c-g-c\right).\)
\(\Rightarrow\) IB = IM (2 cạnh tương ứng).
b) Xét tam giác BAM: AB = AM (gt).
\(\Rightarrow\Delta BAM\) cân tại A.
Mà AI là phân giác \(\widehat{BAM}\) (AI là phân giác \(\widehat{BAC}\), \(M\in AC\)).
\(\Rightarrow\) AI là đường trung trực của BM (T/c tam giác cân).
c) Ta có: AI là đường trung trực của BM (cmt).
\(\Rightarrow\) IB = IM (T/c đường trung trực).
Ta có: \(\widehat{ABI}+\widehat{IBH}=180^o.\\\widehat{AMI} +\widehat{IMC}=180^o.\)
Mà \(\widehat{ABI}=\widehat{AMI}\left(\Delta ABI=\Delta AMI\right).\)
\(\Rightarrow\widehat{IBH}=\widehat{IMC}.\)
Xét tam giác BIH và tam giác MIC:
IB = IM(cmt).
\(\widehat{BIH}=\widehat{MIC}\) (đối đỉnh).
\(\widehat{IBH}=\widehat{IMC}\left(cmt\right).\)
\(\Rightarrow\Delta BIH=\Delta MIC\left(g-c-g\right).\)
\(\Rightarrow\) IH = IC (2 cạnh tương ứng).
d) Ta có: \(AH=AB+BH.\\ AC=AM+MC.\)Mà \(AB=AM\left(cmt\right).\\ BH=MC\left(\Delta BIH=\Delta MIC\right).\)
\(\Rightarrow\) AH = AC.\(\Rightarrow\Delta AHC\) cân tại A.
Mà AI là phân giác \(\widehat{BAC}\left(gt\right).\)
\(\Rightarrow\) AI là đường trung trực của HC (T/c tam giác cân).
e) Ta có:AI vuông góc BM (AI là đường trung trực của BM).
AI vuông góc HC (AI là đường trung trực của HC).
\(\Rightarrow\) BM // HC.

Số ki lô gam ông giảm sau tháng thứ nhất là : 100 : 100 x 10 = 10 ( kg )
Cân nặng của ông sau 1 tháng là : 100 - 10 = 90 ( kg )
Số ki lô gam ông giảm sau tháng thứ 2 là : 90 : 100 x 10= 9 ( kg )
Cân nặng của ông sau 2 tháng là : 90 - 9 = 81 ( kg )
Số ki lô gam ông giảm sau tháng thứ 3 là : 81 : 100 x 10 = 8,1 ( kg )
Cân nặng của ông sau 3 tháng là : 81 - 8,1 = 72,9 ( kg )
K nha mn !

Bài 1:
Mình có hình cho câu a) thôi nha.
a) Xét 2 \(\Delta\) \(ABD\) và \(ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\) (vì D là trung điểm của \(BC\))
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\left(c-c-c\right)\)
=> \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng).
=> \(AD\) là tia phân giác của \(\widehat{BAC}.\)
b) Vì \(\widehat{BAD}=\widehat{CAD}\left(cmt\right)\)
=> \(\widehat{MAD}=\widehat{NAD}.\)
Xét 2 \(\Delta\) \(AMD\) và \(AND\) có:
\(AM=AN\left(gt\right)\)
\(\widehat{MAD}=\widehat{NAD}\left(cmt\right)\)
Cạnh AD chung
=> \(\Delta AMD=\Delta AND\left(c-g-c\right)\)
=> \(\widehat{AMD}=\widehat{AND}\) (2 góc tương ứng).
Mà \(\widehat{AMD}=90^0\left(gt\right)\)
=> \(\widehat{AND}=90^0.\)
=> \(DN\perp AN\)
Hay \(DN\perp AC.\)
Chúc bạn học tốt!



khongcamxuc_123 đó nha bn bn phải giữ lời hứa đấy nha
~~~~ hok tốt ~~~~!!!!
k ngày 3 lần được ko đó hứa nha !