Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
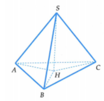
Gọi r 1 , r 2 , r 3 lần lượt là bán kính đường tròn ngoại tiếp Δ H A B , Δ H B C , Δ H C A
Theo định lí Sin, ta có A B sin A H B ⏜ = 2 r 1 ⇒ r 1 = 2 2. sin 150 ° = 2 ; tương tự r 2 = 2 3 3 r 3 = 1
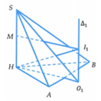
Gọi R 1 , R 2 , R 3 lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp S . H A B , S . H B C , S . H C A
Đặt S H = 2 x ⇒ R 1 = r 1 2 + S H 2 4 = x 2 + 4 ; R 2 = x 2 + 3 4 và R 3 = x 2 + 1
Suy ra ∑ S = S 1 + S 2 + S 3 = 4 π R 1 2 + 4 π R 2 2 + 4 π R 3 2 = 4 π 3 x 2 + 19 3 = 124 π 3 ⇒ x = 2 3 3
Vậy thể tích khối chóp S.ABC là V = 1 3 . S H . S Δ A B C = 1 3 . 4 3 3 . 2 2 3 4 = 4 3
Chú ý: “Cho hình chóp S . A B C có SA vuông góc với đáy và R Δ A B C là bán kính đường tròn ngoại tiếp tam giác A B C → R = R Δ A B C 2 + S A 2 4 là bán kính mặt cầu ngoại tiếp khối chóp S.ABC”

Đáp án B
Tam giác đều cạnh x có bán kính đường tròn ngoại tiếp là
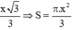
Với mỗi tam giác đề bài cho, độ dài cạnh tam giác sau bẳng 1 2 độ dài cạnh tam giác trước.
Khi đó
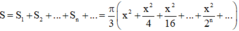
Dễ thấy
![]()
là tổng cấp số nhân lùi vô hạn
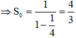
Vậy tổng cần tính là
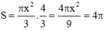


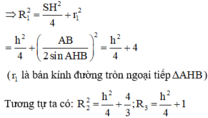





Qua O vẽ OH ⊥ AB và OK ⊥ AD ⇒ OH ⊥ DC, OK ⊥ BC
Gọi I, L lần lượt là giao điểm của OK, OH với DC, BC. Ta có:
+ SABCD = AB.IH = BC.KL
+ SABO = 1/2 AB.OH và SCDO = 1/2 DC.OI
⇒ SABO + SCDO = 1/2 AB.OH + 1/2 DC.OI
= 1/2 AB.OH + 1/2 AB.OI
= 1/2 AB (OH + OI) = 1/2 AB.IH = 1/2 SABCD (1)
+ SBCO = 1/2 BC.OL và SDAO = 1/2 AD.OK
⇒ SBCO + SDAO = 1/2 BC.OL + 1/2AD.OK
= 1/2 BC.OL + 1/2BC.OK
= 1/2BC(OL + OK) = 1/2 BC.KL = 1/2SABCD (2)
Từ (1) và (2) ta có: SABO + SCDO = SBCO + SDAO