Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi r 1 , r 2 , r 3 lần lượt là bán kính đường tròn ngoại tiếp Δ H A B , Δ H B C , Δ H C A
Theo định lí Sin, ta có A B sin A H B ⏜ = 2 r 1 ⇒ r 1 = 2 2. sin 150 ° = 2 ; tương tự r 2 = 2 3 3 r 3 = 1
Gọi R 1 , R 2 , R 3 lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp S . H A B , S . H B C , S . H C A
Đặt S H = 2 x ⇒ R 1 = r 1 2 + S H 2 4 = x 2 + 4 ; R 2 = x 2 + 3 4 và R 3 = x 2 + 1
Suy ra ∑ S = S 1 + S 2 + S 3 = 4 π R 1 2 + 4 π R 2 2 + 4 π R 3 2 = 4 π 3 x 2 + 19 3 = 124 π 3 ⇒ x = 2 3 3
Vậy thể tích khối chóp S.ABC là V = 1 3 . S H . S Δ A B C = 1 3 . 4 3 3 . 2 2 3 4 = 4 3
Chú ý: “Cho hình chóp S . A B C có SA vuông góc với đáy và R Δ A B C là bán kính đường tròn ngoại tiếp tam giác A B C → R = R Δ A B C 2 + S A 2 4 là bán kính mặt cầu ngoại tiếp khối chóp S.ABC”

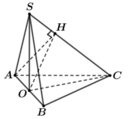
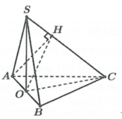
Gọi O là trung điểm của AB![]()
Ta có 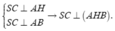
![]()
Trong tam giác vuông SOC có 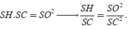
Ta có 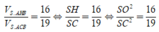
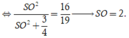
Vậy ![]()
Chọn C.

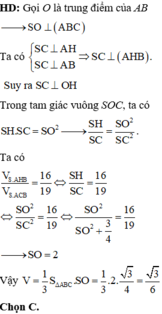
Trong mặt phẳng (ABC), qua A kẻ đường thẳng d song song với BC. Kẻ H I ⊥ d , dễ thấy A I ⊥ S H I . Trong tam giác vuông SHI kẻ H K ⊥ S I , nhận thấy H K ⊥ S I A .
Ta có d S A , B C = d B , S I A = 3 2 d H , S I A = 3 2 H K
Ta tính được H = H A . sin 60 o = a 3 3
Ta có S C H ^ = S C ; A B C ^ , suy ra S H = a 21 3
Từ 1 H K 2 = 1 S H 2 + 1 H I 2 ta thu được H K = a 42 12
Suy ra d S A , B C = 3 2 H K = a 42 8
Đáp án C

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà

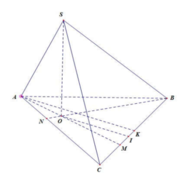

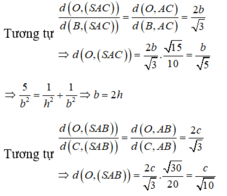
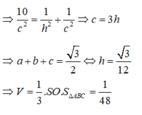
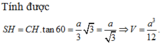
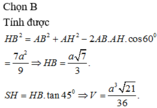
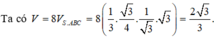
Chọn đáp án B