
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


10³ + 2¹⁵
= 1000 + 32768
= 33768
Mà 33768 : 33 = 1023 (dư 9)
Em xem lại đề

\(\dfrac{2}{x}\) + \(\dfrac{1}{y}\) = \(\dfrac{1}{6}\) (\(x;y\) \(\in\) N*)
\(\dfrac{2}{x}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{y}\)
\(\dfrac{2}{x}\) = \(\dfrac{y-6}{6y}\)
\(x\) = 2: \(\dfrac{y-6}{6y}\)
\(x\) = \(\dfrac{12y}{y-6}\)
Vì \(x\); y \(\in\) N* nên 12\(y\) ⋮ y - 6 ( và y > 6)
12y ⋮ y - 6 ⇔ 12y - 72 + 72 ⋮ y - 6 ⇔ 12.(y-6) + 72 ⋮ y - 6 ⇔ 72⋮ y - 6 72 = 23.32
Ư(72) = { 1; 2; 3; 4; 6; 8; 9; 12; 18; 24; 36; 72}
Lập bảng ta có:
| \(y-6\) | 1 | 2 | 3 | 4 | 6 | 8 | 9 | 12 | 18 | 24 | 36 | 72 |
| y | 7 | 8 | 9 | 10 | 12 | 14 | 15 | 18 | 24 | 30 | 42 | 78 |
| \(x\)=\(\dfrac{12y}{y-6}\) | 84 | 48 | 36 | 30 | 34 | 21 | 20 | 18 | 16 | 15 | 14 | 13 |
Theo bảng trên ta có các cặp số tự nhên \(x\); y thỏa mãn đề bài lần lượt là:
(\(x\);y) =(84;7); (48;8); (36;9); (30;10);(34;12); (21;14); (20;15);(18;18);
(16;24); (15; 30); (14;42);(13;78)
\(\dfrac{2}{x}+\dfrac{1}{y}=\dfrac{1}{6}\left(x;y\inℕ^∗\right)\)
\(\Leftrightarrow\dfrac{2y+x}{xy}=\dfrac{1}{6}\)
\(\Leftrightarrow6\left(2y+x\right)=xy\)
\(\Leftrightarrow12y+6x=xy\)
\(\Leftrightarrow12y-xy+6x=0\)
\(\Leftrightarrow y\left(12-x\right)+6x-72+72=0\)
\(\Leftrightarrow-y\left(x-12\right)+6\left(x-12\right)=-72\)
\(\Leftrightarrow\left(x-12\right)\left(6-y\right)=-72\)
\(\Leftrightarrow\left(x-12\right);\left(6-y\right)\in\left\{-1;1;-2;2;-3;3;-4;4;-8;8;-9;9;-18;18;-24;24;-36;36;-72;72\right\}\)
Lập bảng sẽ ra \(\left(x;y\inℕ^∗\right)\) cần tìm...

Vì \(\left(3x-33\right)^{2016}\ge0;\left|y-7\right|\ge0\Leftrightarrow\left|y-7\right|^{2017}\ge0\)
=>\(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}\ge0\)
mà theo đề bài: \(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}\le0\)
=>\(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}=0\) <=>\(\left(3x-33\right)^{2016}=0;\left|y-7\right|^{2017}=0\)
- (3x-33)2016=0 <=> 3x-33=0 <=> 3x=33 <=> x=11
- |y-7|2017=0 <=> |y-7|=0 <=> y-7=0 <=> y=7
Vậy x=11 và y=7


Kẻ Az//xx'(Az cùng phía Cx' trên nửa mp bờ AC)
\(\Rightarrow\)Az//yy'
\(\Rightarrow\widehat{CAz}=\widehat{ACx}=45^0\) (so le trong)\(;\widehat{zAD}=180^0-\widehat{ADy'}=72^0\)(trong cùng phía)
\(\Rightarrow\widehat{CAD}=\widehat{CAz}+\widehat{zAD}=117^0\)

Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
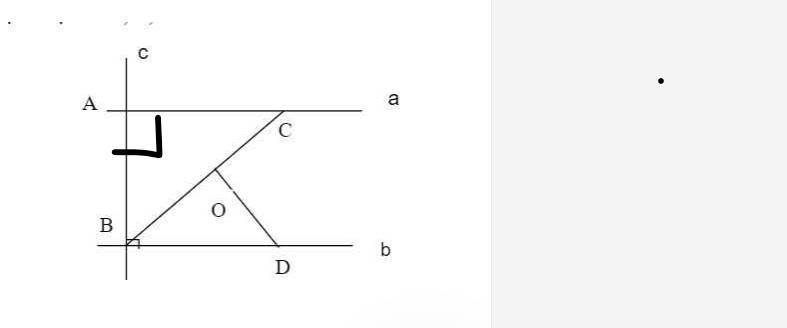
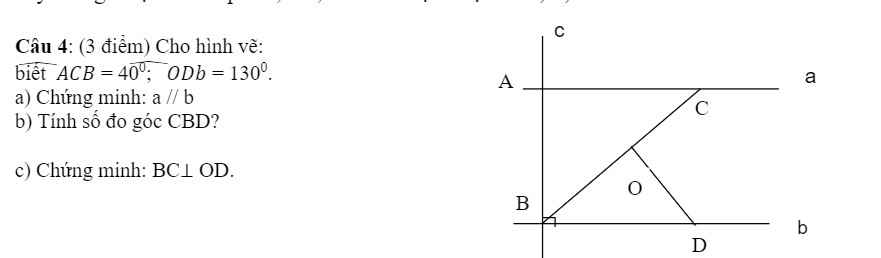
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC

b: Ta có: 2x=3y=5z
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}=\dfrac{x-2y+z}{\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{1}{5}}=\dfrac{14}{\dfrac{1}{30}}=420\)
Do đó: x=210; y=140; z=84

Bài 4:
a: \(C=\left(\dfrac{1}{3}-\dfrac{1}{2}\right)x^3-2x^2-\left(4+1\right)x+1\)
\(=\dfrac{-1}{6}x^3-2x^2-5x+1\)
b: Thay x=2 vào C, ta được:
\(C=\dfrac{-1}{6}\cdot8-2\cdot4-5\cdot2+1=\dfrac{-4}{3}-8-10+1=\dfrac{-4}{3}-17=\dfrac{-4-51}{3}=-\dfrac{55}{3}\)
Bài 5:
Theo đề, ta có: \(\left(xyz\right)^2=2\cdot6\cdot3=36\)
Trường hợp 1: xyz=6
\(\Leftrightarrow\left\{{}\begin{matrix}z=3\\x=1\\y=2\end{matrix}\right.\)
Trường hợp 2: xyz=-6
\(\Leftrightarrow\left\{{}\begin{matrix}z=-3\\x=-1\\y=-2\end{matrix}\right.\)

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
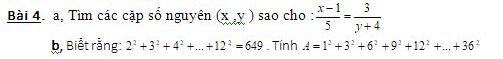 giúp vs ạ:33
giúp vs ạ:33 giúp em với ạ nhanh em cần ạ :33
giúp em với ạ nhanh em cần ạ :33
 mk vs ạ
mk vs ạ Giúp mình với ạ mình cảm ơn:33
Giúp mình với ạ mình cảm ơn:33
a) \(\dfrac{x-1}{5}\)=\(\dfrac{3}{y+4}\)
⇒( x - 1)( y + 4) = 3.5 = (-3)(-5) = 5.3 = (-5)(-3) = 1.15 = (-1)(-15)
Vậy \(\left\{{}\begin{matrix}x=2\\y=11\end{matrix}\right.\); \(\left\{{}\begin{matrix}x=0\\y=-19\end{matrix}\right.\); \(\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\);.........\(\left\{{}\begin{matrix}x=-14\\y=-5\end{matrix}\right.\)
b) A= 1+\(3^2\)+\(2^2\).\(3^3\)+\(3^2\).\(3^2\)+\(3^2\).\(4^2\)+\(3^2\).\(5^2\)+\(3^2\).\(6^2\)+.....\(3^2\).\(12^2\)
=\(3^2\).(\(\dfrac{1}{3}^2\)+\(2^2\)+\(3^2\)+\(4^2\)+\(5^2\)+\(6^2\)+......+\(12^2\))
=9.(\(\dfrac{1}{9}\)+649)=5842
b) Vì \(2^2+3^2+...+12^2=649\)
\(=>3^2\left(2^2+3^2+...+12^2\right)=3^2\cdot649\)
\(=>6^2+9^2+...+36^2=5841\)
=> A = \(1+9+5841\) = 5851