K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
2
AH
Akai Haruma
Giáo viên
1 tháng 12 2021
Những bài này bạn cứ đối chiếu với hằng đẳng thức đáng nhớ thôi.
Lời giải:
a. $x^2+4xy+4y^2=(x+2y)^2$
b. $4x^2-12xy+9y^2=(2x-3y)^2$
c. $9x^2-12xy+4y^2=(3x-2y)^2$
d. $x^2+6xy+9y^2=(x+3y)^2$
e. $x^3-6x^2y+12xy^2-8y^3=(x-2y)^3$
f. $-27x^3+27x^2y-9xy^2+y^3=(-3x+y)^3$
CD
1 tháng 12 2021
a, 2xy -> 4xy
b, x2 -12xy + y2 -> 4x2 -12xy + 9y2
c, (2x-3y)2 -> (3x-2y)2
d, (x+3y)2 -> (x-3y)2
Chúc bạn học tốt nhé!
10 tháng 11 2021
Bài 2:
\(a,=x\left(x+7\right)\\ b,=x\left(x^2+4x+4\right)=x\left(x+2\right)^2\)
Bài 3:
\(a,\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\\ b,\Leftrightarrow x^2-x-2x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Bài 4:
\(a,\widehat{D}=360^0-\widehat{A}-\widehat{B}-\widehat{C}=150^0\)
\(b,\dfrac{x+10}{2}=12\Leftrightarrow x+10=24\Leftrightarrow x=14\left(cm\right)\)
19 tháng 6 2023
2:
Gọi số sách lúc đầu ở tủ 1 và tủ 2 lần lượt là a,b
Theo đề, ta có:
a+b=600 và a-80=1/2(b+80)
=>a=280 và b=320
10 tháng 5 2022
a.\(A=\left(\dfrac{x^2-3}{x^2-9}+\dfrac{1}{x-3}\right):\dfrac{x}{x+3}\)
\(A=\left(\dfrac{x^2-3+\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{x}{x+3}\)
\(A=\left(\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\right).\dfrac{x+3}{x}\)
\(A=\dfrac{\left(x^2+x\right)\left(x+3\right)}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x\left(x+1\right)\left(x+3\right)}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x+1}{x-3}\)
b.\(A=3\)
\(\Leftrightarrow\dfrac{x+1}{x-3}=3\)
\(\Leftrightarrow\dfrac{x+1}{x-3}=\dfrac{3\left(x-3\right)}{x-3}\)
\(\Leftrightarrow x+1=3\left(x-3\right)\)
\(\Leftrightarrow x+1=3x-9\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\left(tm\right)\)
Vậy \(x=5\) thì \(A=3\)
31 tháng 1
a: \(\dfrac{-2}{x^2+6x}=\dfrac{-2}{x\left(x+6\right)}\)
\(\dfrac{x}{x+6}=\dfrac{x\cdot x}{x\left(x+6\right)}=\dfrac{x^2}{x\left(x+6\right)}\)
b: \(\dfrac{11}{25-x^2}=\dfrac{-11}{x^2-25}=\dfrac{-11}{\left(x-5\right)\left(x+5\right)}=\dfrac{-11\left(x-5\right)}{\left(x-5\right)^2\cdot\left(x+5\right)}\)
\(\dfrac{2}{x^2-10x+25}=\dfrac{2}{\left(x-5\right)^2}=\dfrac{2\left(x+5\right)}{\left(x+5\right)\cdot\left(x-5\right)^2}\)
2
10 tháng 5 2022
`[x+1]/2021+[x+2]/2020+[x+3]/2019+[x+4]/2018=-4`
`<=>[x+1]/2021+1+[x+2]/2020+1+[x+3]/2019+1+[x+4]/2018+1=-4+4`
`<=>[x+1+2021]/2021+[x+2+2020]/2020+[x+3+2019]/2019+[x+4+2018]/2018=0`
`<=>[x+2022]/2021+[x+2022]/2020+[x+2022]/2019+[x+2022]/2018=0`
`<=>(x+2022)(1/2021+2020+1/2019+1/2018)=0`
Mà `1/2021+2020+1/2019+1/2018 \ne 0`
`=>x+2022=0`
`<=>x=-2022`
Vậy `S={-2022}`
17 tháng 2 2022
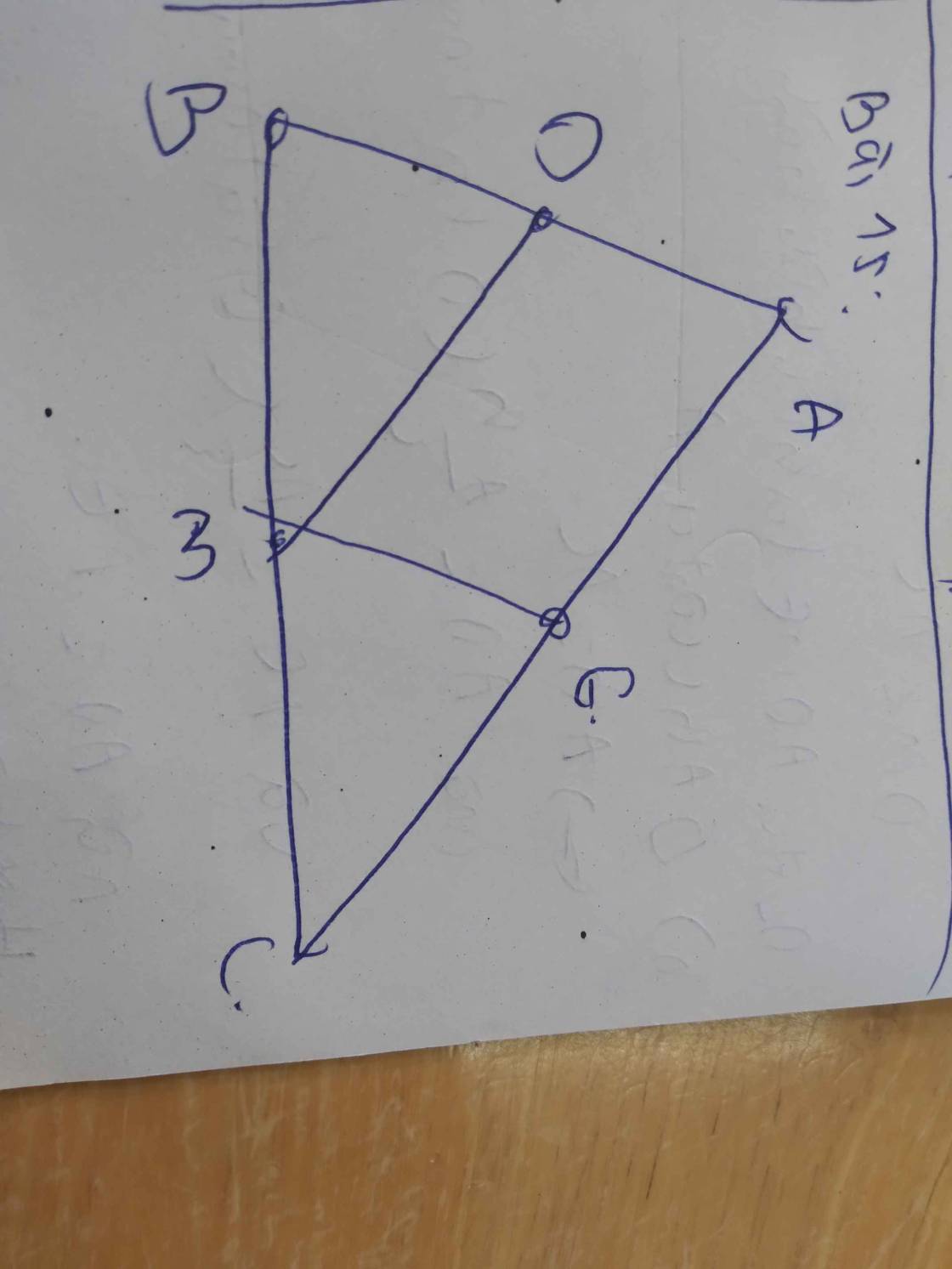
Bài 2:
Xét ΔBDC có BE/ED=BF/FC
nên EF//DC
mà DC//AB
nên EF//AB
11 tháng 3 2022
a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH∼ΔBDA
b: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD∼ΔHBA
Suy ra: HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)
11 tháng 3 2022
a) Xét \(\Delta ADH\) và \(\Delta BDA:\)
\(\widehat{H}=\widehat{A}\left(=90^o\right).\)
\(\widehat{D}\) chung.
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g-g\right).\)
b) Xét \(\Delta BDA\) và \(\Delta BAH:\)
\(\widehat{BAD}=\widehat{BHA}\left(=90^o\right).\)
\(\widehat{B}\) chung.
\(\Rightarrow\Delta BDA\sim\) \(\Delta BAH\left(g-g\right).\)
Mà \(\Delta ADH\sim\Delta BDA\left(cmt\right).\)
\(\Rightarrow\Delta ADH\sim\Delta BAH.\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{DH}{AH}\) (2 cạnh tương ứng).
\(\Rightarrow AH^2=DH.BH.\)
B
4 tháng 4 2023
`x/40 - x/50 =0,3`
`<=> x/40-x/50 =3/10`
`<=> (5x)/200 - (4x)/200 = 60/200`
`<=> 5x-4x=60`
`<=>x=60`
Vậy phương trình có nghiệm `x=60`
4 tháng 4 2023
\(\dfrac{x}{40}-\dfrac{x}{50}=0,3\)
\(\Leftrightarrow\dfrac{55x}{200}-\dfrac{4x}{200}=\dfrac{60}{200}\)
\(\Leftrightarrow x=60\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{60\right\}\)
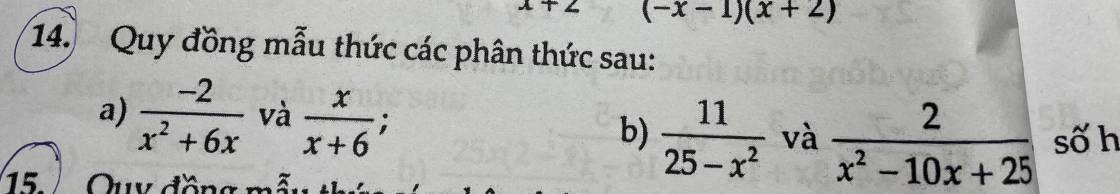
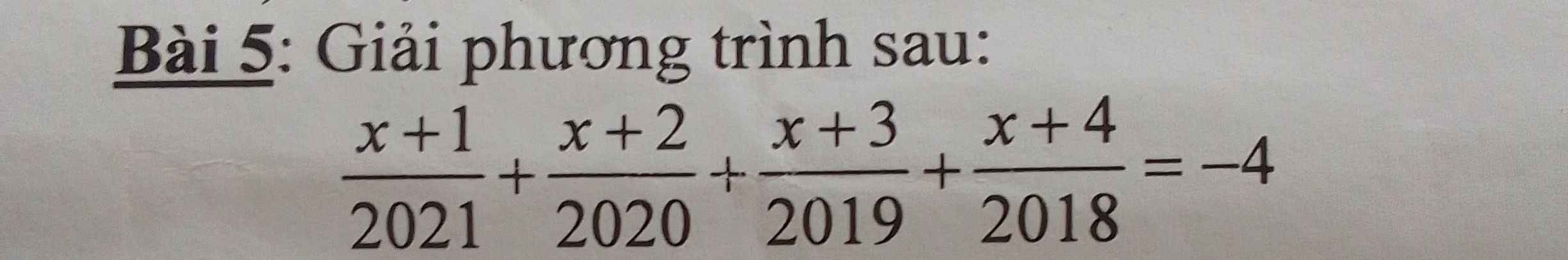
wtf wtf em lop 4
HÌNH GÌ VẬY