K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 1
a: \(\dfrac{-2}{x^2+6x}=\dfrac{-2}{x\left(x+6\right)}\)
\(\dfrac{x}{x+6}=\dfrac{x\cdot x}{x\left(x+6\right)}=\dfrac{x^2}{x\left(x+6\right)}\)
b: \(\dfrac{11}{25-x^2}=\dfrac{-11}{x^2-25}=\dfrac{-11}{\left(x-5\right)\left(x+5\right)}=\dfrac{-11\left(x-5\right)}{\left(x-5\right)^2\cdot\left(x+5\right)}\)
\(\dfrac{2}{x^2-10x+25}=\dfrac{2}{\left(x-5\right)^2}=\dfrac{2\left(x+5\right)}{\left(x+5\right)\cdot\left(x-5\right)^2}\)
2
10 tháng 5 2022
`[x+1]/2021+[x+2]/2020+[x+3]/2019+[x+4]/2018=-4`
`<=>[x+1]/2021+1+[x+2]/2020+1+[x+3]/2019+1+[x+4]/2018+1=-4+4`
`<=>[x+1+2021]/2021+[x+2+2020]/2020+[x+3+2019]/2019+[x+4+2018]/2018=0`
`<=>[x+2022]/2021+[x+2022]/2020+[x+2022]/2019+[x+2022]/2018=0`
`<=>(x+2022)(1/2021+2020+1/2019+1/2018)=0`
Mà `1/2021+2020+1/2019+1/2018 \ne 0`
`=>x+2022=0`
`<=>x=-2022`
Vậy `S={-2022}`
11 tháng 3 2022
a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH∼ΔBDA
b: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD∼ΔHBA
Suy ra: HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)
11 tháng 3 2022
a) Xét \(\Delta ADH\) và \(\Delta BDA:\)
\(\widehat{H}=\widehat{A}\left(=90^o\right).\)
\(\widehat{D}\) chung.
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g-g\right).\)
b) Xét \(\Delta BDA\) và \(\Delta BAH:\)
\(\widehat{BAD}=\widehat{BHA}\left(=90^o\right).\)
\(\widehat{B}\) chung.
\(\Rightarrow\Delta BDA\sim\) \(\Delta BAH\left(g-g\right).\)
Mà \(\Delta ADH\sim\Delta BDA\left(cmt\right).\)
\(\Rightarrow\Delta ADH\sim\Delta BAH.\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{DH}{AH}\) (2 cạnh tương ứng).
\(\Rightarrow AH^2=DH.BH.\)
B
4 tháng 4 2023
`x/40 - x/50 =0,3`
`<=> x/40-x/50 =3/10`
`<=> (5x)/200 - (4x)/200 = 60/200`
`<=> 5x-4x=60`
`<=>x=60`
Vậy phương trình có nghiệm `x=60`
4 tháng 4 2023
\(\dfrac{x}{40}-\dfrac{x}{50}=0,3\)
\(\Leftrightarrow\dfrac{55x}{200}-\dfrac{4x}{200}=\dfrac{60}{200}\)
\(\Leftrightarrow x=60\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{60\right\}\)
MH
30 tháng 3 2022
a) \(\left|7x-4\right|=-7\)
Mà \(\left|7x-4\right|\ge0\forall x\)
\(\Rightarrow\) phương trình vô nghiệm
b) \(\left|3x-4\right|=\left|7x+5\right|\)
\(\Rightarrow\left[{}\begin{matrix}3x-4=7x+5\\3x-4=-7x-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{9}{4}\\x=-\dfrac{1}{10}\end{matrix}\right.\)
Vậy ...
19 tháng 12 2023
a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP
3 tháng 5 2022
Câu 9:
a. <=> 4x= 12
<=> x=3
S={3}
b. <=> (2x-6).(x+9)=0
<=> 2x-6=0 hoặc x+9=0
<=> x= 3 hoặc x=-9
S={3;-9}
c. <=> 5x=-20
<=> x= -4
S={-4}
d. <=> (2x-6).(3x+9)=0
<=> 2x-6=0 hoặc 3x+9=0
<=> 2x=6 hoặc 3x=-9
<=> x=3 hoặc x= -3
S={3;-3}
e. th1: 2x-3= 6x+5 nếu 2x-3>0 => x>\(\dfrac{3}{2}\)
2x-3=6x+5
<=>2x-6x= 5+3
<=>-4x=8
<=> x= -2 (loại)
th2: 2x-3= -6x+5 nếu 2x-3<0 => x<\(\dfrac{3}{2}\)
2x-3=-6x+5
<=>2x+6x= 5+3
<=>8x=8
<=>x=1 (chọn)
S={1}
f. <=> -12x>6
<=> x< -\(\dfrac{1}{2}\)
S={x/x<-\(\dfrac{1}{2}\)}
g. th1: 2x+3=4x+5 nếu 2x+3>0 => x>\(\dfrac{-3}{2}\)
2x+3=4x+5
2x-4x=5-3
-2x= 2
x= -1 (chọn)
th2: 2x+3=-4x+5 nếu 2x+3<0 => x<\(\dfrac{-3}{2}\)
2x+3=-4x+5
2x+4x= 5-3
6x=2
x= \(\dfrac{1}{3}\)(loại)
S={-1}
h. <=> -2x>-6
<=> x< 3
S={x/x<3}
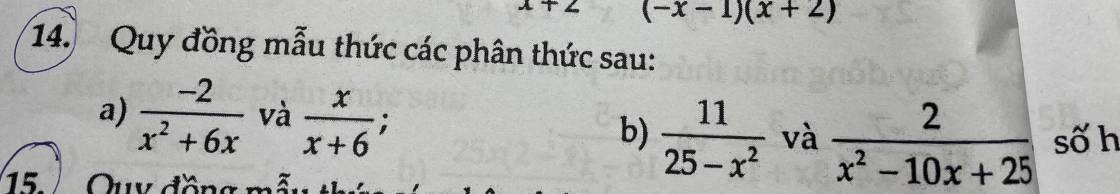
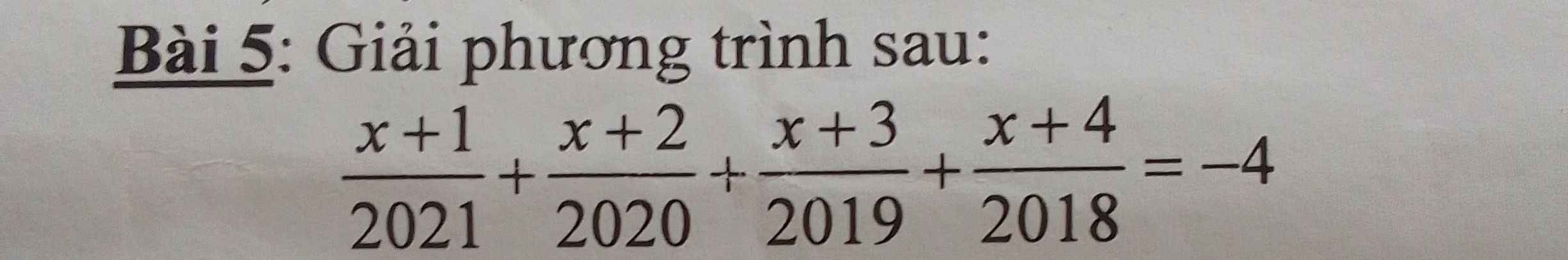
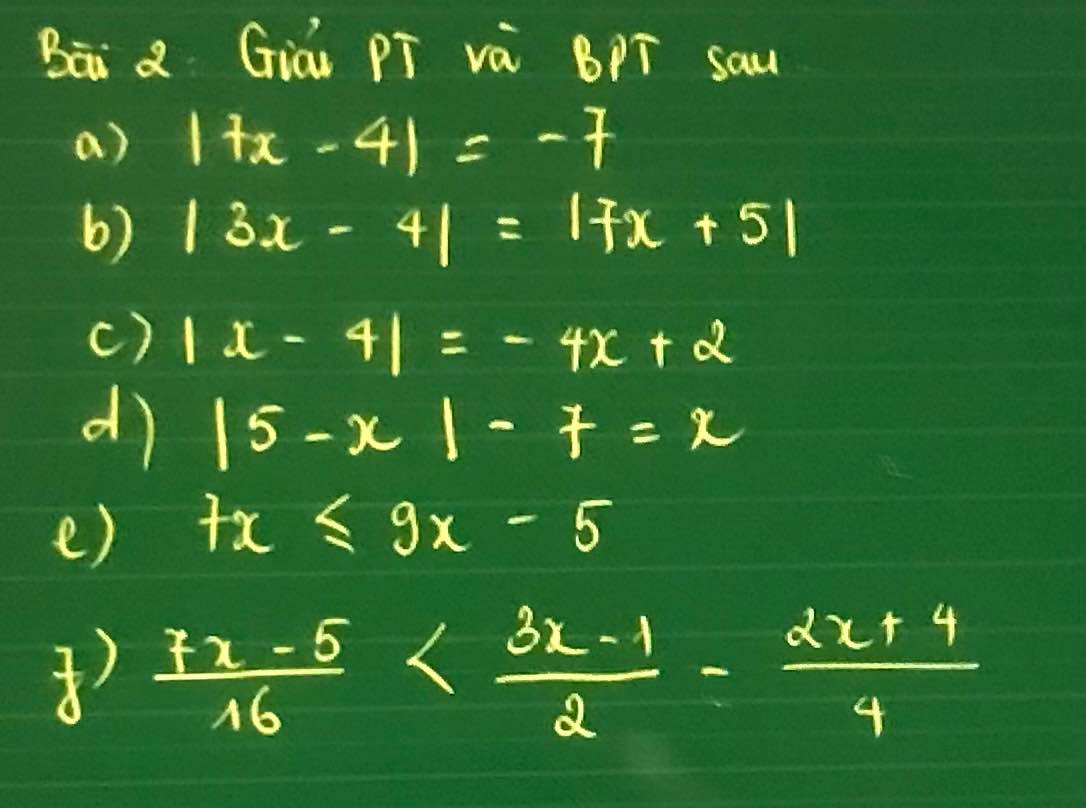
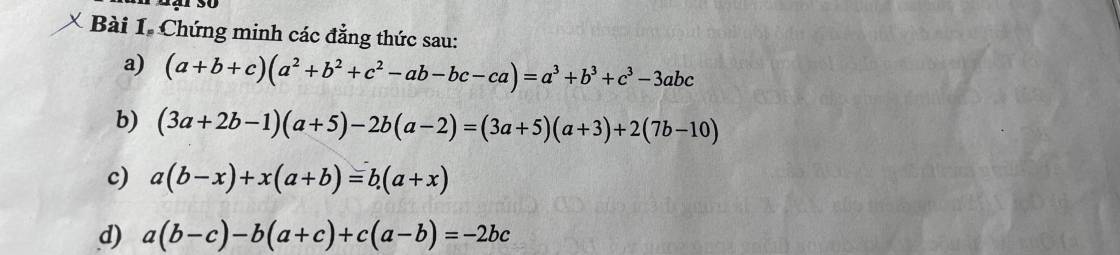
Bài 2:
Xét ΔBDC có BE/ED=BF/FC
nên EF//DC
mà DC//AB
nên EF//AB